
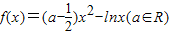
 (x>0),求导函数,确定函数在(0,e]上的单调性,从而可求函数的最小值;
(x>0),求导函数,确定函数在(0,e]上的单调性,从而可求函数的最小值; <0在区间(1,+∞)上恒成立,分类讨论,即可求得实数a的取值范围.
<0在区间(1,+∞)上恒成立,分类讨论,即可求得实数a的取值范围. (x>0),∴
(x>0),∴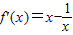
 ;
; <0在区间(1,+∞)上恒成立
<0在区间(1,+∞)上恒成立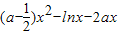 ,则g′(x)=(x+1)(2a-1-
,则g′(x)=(x+1)(2a-1- )
) <1
<1 ,g′(x)<0,函数在(1,+∞)上为减函数,∴g(x)<g(1)=-
,g′(x)<0,函数在(1,+∞)上为减函数,∴g(x)<g(1)=- -a,
-a, -a≤0,即-
-a≤0,即- ≤a≤
≤a≤ 时,g(x)<0恒成立;
时,g(x)<0恒成立; <a<1时,令g′(x)=0,得x=
<a<1时,令g′(x)=0,得x= >1,函数在(1,
>1,函数在(1,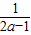 )上为减函数,(
)上为减函数,( ,+∞)为增函数,
,+∞)为增函数, ),+∞),不合题意;
),+∞),不合题意; ≤a≤
≤a≤ 时,g(x)<0恒成立
时,g(x)<0恒成立 ].
].

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:2012-2013学年山东省高三上学期期末模块考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数
(I)当a=1时,求函数 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式;
(II)当a=2时,在 的条件下,求
的条件下,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市高三上学期期中考试数学(解析版) 题型:解答题
(本题满分16分)
已知函数
(I)当a=2时,求函数 的最大值和最小值;
的最大值和最小值;
(II)若函数 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(III)当a=1时,求证:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省唐山市高三下学期第二次模拟考试数学理卷 题型:解答题
(本小题满分12分)
已知函数
(I)当a=1时,求 的最小值;
的最小值;
(II)求证: 在区间(0,1)单调递减。
在区间(0,1)单调递减。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com