
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断
,判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 在
在![]() 上的最小值;
上的最小值;
(3)若![]() ,
,![]() ,
,![]() 有三个不同实根,求
有三个不同实根,求![]() 的取值范围.
的取值范围.
【答案】(1)奇函数;(2)0;(3)![]() .
.
【解析】
(1)由![]() 判断即可得解;
判断即可得解;
(2)由分段函数求值域问题分![]() ,
,![]() ,
,![]() ,
,![]() ,讨论即可;
,讨论即可;
(3)由方程与函数的关系可得![]() 有三个不同实根,等价于函数
有三个不同实根,等价于函数![]() 与直线
与直线![]() 有三个交点,通过求函数
有三个交点,通过求函数![]() 的单调性及值域即可得解.
的单调性及值域即可得解.
解:(1)当![]() 时,
时,![]() ,
,
则![]() ,
,
故![]() 为奇函数;
为奇函数;
(2)当![]() 时,
时,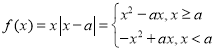 ,
,
又![]() ,
,
①当![]() 时,可得函数
时,可得函数![]() 在
在![]() 为增函数,可得
为增函数,可得![]() ;
;
②当![]() 时,可得函数
时,可得函数![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
由![]() ,
,
可得当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
③当![]() 时,由
时,由![]() ,可得
,可得![]() ;
;
综上可得:当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值为即
上的最小值为即![]() ;
;
(3)因为![]() ,且
,且![]() 有三个不同实根,
有三个不同实根,
则函数![]() 不单调,且
不单调,且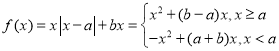 ,
,
因为![]() ,又
,又![]() ,
,![]() ,
,
所以当![]() 时,函数为增函数,则
时,函数为增函数,则![]() 时,函数不单调,要使函数
时,函数不单调,要使函数![]() 有三个不同实根,则
有三个不同实根,则![]() ,即
,即![]() ,即
,即![]() ,
,
故![]() ,
,
故![]() 的取值范围为:
的取值范围为:![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】若椭圆C1: ![]() 和椭圆C2:
和椭圆C2: ![]() 的焦点相同且a1>a2.给出如下四个结论:
的焦点相同且a1>a2.给出如下四个结论:
①椭圆C1和椭圆C2一定没有公共点;
②![]() ;
;
③![]() ;
;
④a1-a2<b1-b2.
其中,所有正确结论的序号是( )
A. ②③④ B. ①③④
C. ①②④ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古建筑中的窗饰是艺术和技术的统一体,给人于美的享受.如图(1)为一花窗;图(2)所示是一扇窗中的一格,呈长方形,长30 cm,宽26 cm,其内部窗芯(不含长方形边框)用一种条形木料做成,由两个菱形和六根支条构成,整个窗芯关于长方形边框的两条对称轴成轴对称.设菱形的两条对角线长分别为x cm和y cm,窗芯所需条形木料的长度之和为L.
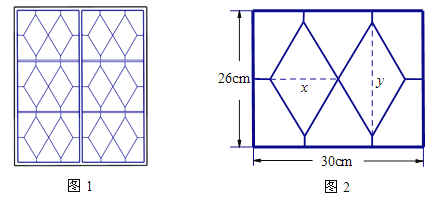
(1)试用x,y表示L;
(2)如果要求六根支条的长度均不小于2 cm,每个菱形的面积为130 cm2,那么做这样一个窗芯至少需要多长的条形木料(不计榫卯及其它损耗)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.平行的两条直线的斜率一定存在且相等
B.平行的两条直线的倾斜角一定相等
C.垂直的两条直线的斜率之积为一1
D.只有斜率都存在且相等的两条直线才平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图(1)为东方体育中心,其设计方案侧面的外轮廓线如图(2)所示;曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() 且
且![]() 恰好等于圆
恰好等于圆![]() 的半径,
的半径,![]() 与圆相切且
与圆相切且![]() .
.
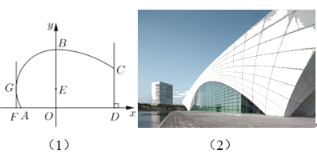
(1)若要求![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)当![]() 时,若要求
时,若要求![]() 不超过45米,求
不超过45米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.在线性回归分析中,相关系数r的值越大,变量间的相关性越强
B.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.在问归分析中,![]() 为0.98的模型比
为0.98的模型比![]() 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5张奖券中有2张是中奖的,先由甲抽1张,然后由乙抽1张,抽后不放回,求:
(1)甲中奖的概率![]() ;
;
(2)甲、乙都中奖的概率![]() ;
;
(3)只有乙中奖的概率![]() ;
;
(4)乙中奖的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为宣传本市,随机对本市内![]() 岁的人群抽取了
岁的人群抽取了![]() 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |

(1)分别求出![]() 的值;
的值;
(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com