
(1)求证:直线与抛物线总有两个交点;
(2)设直线与抛物线的交点为Q、R,OQ⊥OR,求p关于m的函数f(m)的表达式;
(3)(文)在(2)的条件下,若抛物线焦点F到直线x+y=m的距离为![]() ,求此直线的方程;
,求此直线的方程;
(理)在(2)的条件下,若m变化,使得原点O到直线QR的距离不大于![]() ,求p的值的范围.
,求p的值的范围.
| 解:(1)抛物线y2=p(x+1)的准线方程是x=-1- 由 得x2-(2m+p)x+(m2-p)=0. 而判别式Δ=(2m+p)2-4(m2-p)=p(4m+p+4). 又p>0及4m+p+4>0,可知Δ>0. 因此,直线与抛物线总有两个交点; (2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),由(1)知,x1、x2是方程x2-(2m+p)x+m2-p=0的两根, ∴x1+x2=2m+p,x1·x2=m2-p. 由OQ⊥OR,得kOQ·kOR=-1, 即有x1x2+y1y2=0. 又Q、R为直线x+y=m上的点, 因而y1=-x1+m,y2=-x2+m. 于是x1x2+y1y2=2x1x2-m(x1+x2)+m2=2(m2-p)-m(2m+p)+m2=0, ∴p=f(m)= 由 (3)(文)由于抛物线y2=p(x+1)的焦点F坐标为(-1+
又p= 解得m1=0,m2=- 但m≠0且m>-2,因而舍去m1、m2、m3,故所求直线方程为3x+3y+4=0. (理)解法一:由于原点O到直线x+y=m的距离不大于
由(2),知m>-2且m≠0, 故m∈[-1,0)∪(0,1]. 由(2),知f(m)= 当m∈[-1,0)时,任取m1、m2,0>m1>m2≥-1,则 f(m1)-f(m2)=(m1-m2)+( =(m1-m2)[1- 由0>m1>m2≥-1,知0<(m1+2)(m2+2)<4,1- 又由m1-m2>0知f(m1)<f(m2)因而f(m)为减函数. 可见,当m∈[-1,0)时,p∈(0,1]. 同样可证,当m∈(0,1]时,f(m)为增函数,从而p∈(0, 解法二:由解法一知,m∈[-1,0)∪(0,1].由(2)知 p=f(m)= 设t= g(t)=2t2+t=2(t+ ∴当t∈(-∞,-1]时,g(t)为减函数,g(t)∈[1,+∞). 当t∈[1,+∞)时,g(t)为增函数,g(t)∈[3,+∞). 因此,当m∈[-1,0]时,t∈(-∞,-1],p= 当m∈(0,1]时,t∈[1,+∞),p∈(0, |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,求p的值的范围.
,求p的值的范围.查看答案和解析>>
科目:高中数学 来源:2007-2008学年福建省莆田四中高二(上)模块数学试卷(理科)(解析版) 题型:解答题
 ,求p的值的范围.
,求p的值的范围.查看答案和解析>>
科目:高中数学 来源:2007-2008学年福建省莆田四中高二(上)模块数学试卷(文科)(解析版) 题型:解答题
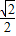 ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com