
已知函数 的定义域为
的定义域为 ,且
,且 ,
, ,
,
当 ,
,
 且
且 ,时
,时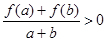 恒成立.
恒成立.
(1)判断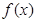 在
在 上的单调性;
上的单调性;
(2)解不等式 ;
;
(3)若 对于所有
对于所有 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)详见解析;(2) ;(3)
;(3)
解析试题分析:(1)将 赋予
赋予 ,即将
,即将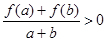 转化为
转化为 ,根据
,根据 可知
可知 ,即
,即 ,根据单调性的定义可得函数
,根据单调性的定义可得函数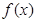 在
在 上的单调性。(2)由(1)知
上的单调性。(2)由(1)知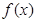 在
在 上是单调增函数,根据单调性可得自变量的大小关系,同时自变量应在所给的定义域内,有以上不等式组组成的不等式组可得所求不等式的解集。(3)
上是单调增函数,根据单调性可得自变量的大小关系,同时自变量应在所给的定义域内,有以上不等式组组成的不等式组可得所求不等式的解集。(3) 恒成立即
恒成立即 恒成立,用函数
恒成立,用函数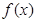 的单调性可求其最值。将问题转化为关于
的单调性可求其最值。将问题转化为关于 的一元二次不等式恒成立问题,因为
的一元二次不等式恒成立问题,因为 ,又可将上式看成关于
,又可将上式看成关于 的一次不等式,讨论单调性即可得出。
的一次不等式,讨论单调性即可得出。
试题解析:解:(1)∵当 ,
,
 且
且 ,时
,时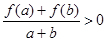 恒成立,
恒成立,
∴ , ∴
, ∴  , 2分
, 2分
∴ 时,∴
时,∴  ,
, 时,∴
时,∴  4分
4分
∴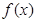 在
在 上是单调增函数 5分
上是单调增函数 5分
(2)∵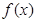 在
在 上是单调增函数,且
上是单调增函数,且
∴  , 7分
, 7分
解得  8分
8分
故所求不等式的解集  9分
9分
(3)∵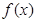 在
在 上是单调增函数,
上是单调增函数, ,
,
∴ , 10分
, 10分
若 对于所有
对于所有 ,
, 恒成立,
恒成立,
则 ,
, 恒成立, 11分
恒成立, 11分
即 ,
, 恒成立,
恒成立,
令 ,
,
要使 在
在 恒成立,
恒成立,
则必须 ,解得
,解得 ,或
,或 13分
13分
则 的取值范围是
的取值范围是 14分
14分
考点:1函数单调性的定义;2用单调性求函数的最值。


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
判断下列对应是否是从集合A到集合B的函数.
(1) A=B=N*,对应法则f:x→y=|x-3|,x∈A,y∈B;
(2) A=[0,+∞),B=R,对应法则f:x→y,这里y2=x,x∈A,y∈B;
(3) A=[1,8],B=[1,3],对应法则f:x→y,这里y3=x,x∈A,y∈B;
(4) A={(x,y)|x、y∈R},B=R,对应法则:对任意(x,y)∈A,(x,y)→z=x+3y,z∈B.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)= 其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个不相同的实数根,求a取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=ax-(1+a2)x2,其中a>0,区间I={x|f(x)>0}.
(1)求I的长度(注:区间(α,β)的长度定义为β-α);
(2)给定常数k∈(0,1),当1-k≤a≤1+k时,求I的长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com