
(本小题满分12分)
已知数列 的相邻两项
的相邻两项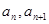 是关于
是关于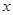 的方程
的方程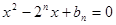
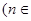 N
N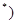 的两根,且
的两根,且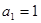 .
.
(1) 求数列 和
和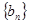 的通项公式;
的通项公式;
(2) 设 是数列
是数列 的前
的前 项和, 问是否存在常数
项和, 问是否存在常数 ,使得
,使得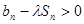 对任意
对任意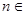 N
N 都成立,若存在, 求出
都成立,若存在, 求出 的取值范围; 若不存在, 请说明理由.
的取值范围; 若不存在, 请说明理由.
(1) ,
,
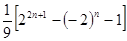 。(2)
。(2) 。
。
解析试题分析:(1) ∵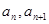 是关于
是关于 的方程
的方程
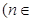 N
N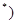 的两根,
的两根,
∴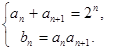
由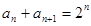 ,得
,得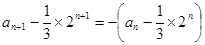 ,
,
故数列 是首项为
是首项为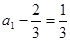 ,公比为
,公比为 的等比数列.
的等比数列.
∴ , 即
, 即 . 所以
. 所以
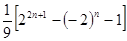 。
。
(2)
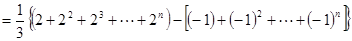
 .、
.、
要使 对任意
对任意 N
N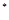 都成立,
都成立,
即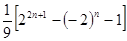
 (*)对任意
(*)对任意 N
N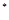 都成立.
都成立.
当 为正奇数时, 由(*)式得
为正奇数时, 由(*)式得
 ,
,
即
 ,∵
,∵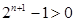 , ∴
, ∴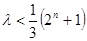 对任意正奇数
对任意正奇数 都成立.当且仅当
都成立.当且仅当 时,
时, 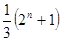 有最小值
有最小值 . ∴
. ∴ .
.
② 当 为正偶数时, 由(*)式得
为正偶数时, 由(*)式得
 ,
,
即
 ,∵
,∵ ,∴
,∴ 对任意正偶数
对任意正偶数 都成立.
都成立.
当且仅当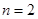 时,
时, 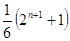 有最小值
有最小值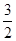 . ∴
. ∴
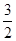 . ……12分
. ……12分
综上所述, 存在常数 ,使得
,使得 对任意
对任意 N
N 都成立,
都成立,  的取值范围是
的取值范围是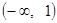 .
.
考点:数列通项公式的求法;数列前n项和的求法。
点评:本题主要考查用待定系数法求数列的通项公式和用分组求和法求数列的前n项和,属于常规题型。第二问主要体现了分类讨论的数学思想,属于难点。若已知递推式 的形式求数列的通项公式,一般来说要在原递推式两边同除以
的形式求数列的通项公式,一般来说要在原递推式两边同除以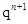 来构造。
来构造。


科目:高中数学 来源: 题型:解答题
下图是一个按照某种规律排列出来的三角形数阵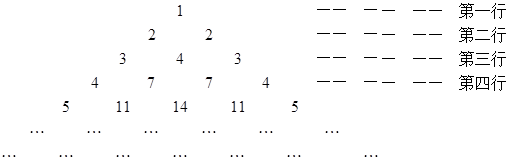
假设第 行的第二个数为
行的第二个数为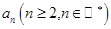
(1)依次写出第七行的所有7个数字(不必说明理由);
(2)写出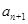 与
与 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出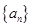 的通项公式
的通项公式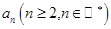 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
对数列{an},规定{△an}为数列{an}的一阶差分数列,其中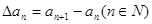 。
。
对自然数k,规定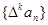 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中 。
。
(1)已知数列{an}的通项公式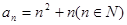 ,试判断
,试判断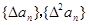 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列{an}首项a1=1,且满足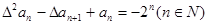 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
(3)对(2)中数列{an},是否存在等差数列{bn},使得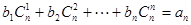 对一切自然
对一切自然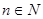 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)在数列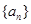 中,
中,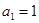 ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有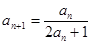 .
.
(1)证明数列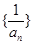 为等差数列,并求
为等差数列,并求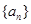 的通项公式;
的通项公式;
(2)设数列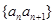 的前n项和为
的前n项和为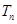 ,求使得
,求使得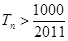 的最小正整数
的最小正整数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数列{an}满足4a1=1,an-1=[(-1)nan-1-2]an(n≥2),(1)试判断数列{1/an+(-1)n}是否为等比数列,并证明;(2)设an2?bn=1,求数列{bn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com