
| ||||
| 2h |
| ||
| 12 |


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源:高中新教材同步教学·高一数学 题型:013
给出以下四个命题:
①(x-a)(x-2a)≤0且x≠a; ②(x-a)(x-2a)<0或x=2a;
③a≤x≤2a; ④a<x≤2a.
其中与关于x的方程![]() ≤0等价的有
≤0等价的有
[ ]
查看答案和解析>>
科目:高中数学 来源: 题型:013
给出以下四个命题:
①(x-a)(x-2a)≤0且x≠a; ②(x-a)(x-2a)<0或x=2a;
③a≤x≤2a; ④a<x≤2a.
其中与关于x的方程![]() ≤0等价的有
≤0等价的有
[ ]
查看答案和解析>>
科目:高中数学 来源:2012届福建省福州市高二期末理科考试数学试卷 题型:填空题
以下四个命题:
① x=0是函数f (x)=x3+2的极值点;
② 当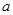 无限趋近于0时,
无限趋近于0时,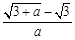 无限趋近于
无限趋近于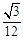 ;
;
③ ¬q是¬p的必要不充分条件,则p是q的充分不必要条件;
④在ΔABC中,“A>30º ”是“sinA>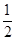 ”的必要不充分。
”的必要不充分。
其中真命题的序号为 (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
①f(x)=![]() 在[0,1]上连续;
在[0,1]上连续;
②若f(x)是(a,b)内的连续函数,则f(x)在(a,b)内有最大值和最小值;
③![]()
![]() =4;
=4;
④若f(x)=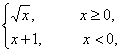 则
则![]() f(x)=0.
f(x)=0.
其中正确命题的序号是__________________.(请把你认为正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com