
如图,线段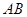 过y轴上一点
过y轴上一点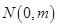 ,
,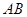 所在直线的斜率为
所在直线的斜率为 ,两端点
,两端点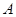 、
、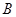 到y轴的距离之差为
到y轴的距离之差为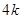 .
.
(Ⅰ)求出以y轴为对称轴,过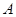 、
、 、
、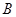 三点的抛物线方程;
三点的抛物线方程;
(Ⅱ)过抛物线的焦点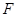 作动弦
作动弦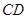 ,过
,过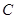 、
、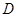 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为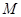 ,求点
,求点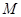 的轨迹方程,并求出
的轨迹方程,并求出 的值.
的值.
(Ⅰ)抛物线方程为 ; (Ⅱ)
; (Ⅱ) 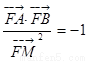 。
。
【解析】(I) 设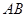 所在直线方程为
所在直线方程为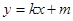 ,抛物线方程为
,抛物线方程为
且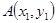 ,
,
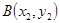 ,
,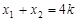 ,再让直线AB的方程与抛物线的方程联立,借助韦达定理建立关于p的方程,求出p值,确定出抛物线的方程.
,再让直线AB的方程与抛物线的方程联立,借助韦达定理建立关于p的方程,求出p值,确定出抛物线的方程.
(II) 设 ,
, ,然后利用导数求出经过C、D的切线方程,求出交点M的坐标,设
,然后利用导数求出经过C、D的切线方程,求出交点M的坐标,设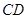 的直线方程为
的直线方程为 ,代入
,代入 得
得 ,根据
,根据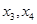 是方程
是方程 的两个根,确定点M的轨迹方程以后,解决此问题才有了正确的出口.
的两个根,确定点M的轨迹方程以后,解决此问题才有了正确的出口.
(Ⅰ)设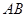 所在直线方程为
所在直线方程为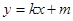 ,抛物线方程为
,抛物线方程为 ,且
,且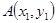 ,
,
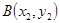 ,不妨设
,不妨设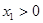 ,
,
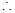
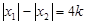 即
即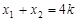
把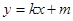 代入
代入 得
得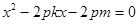
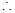

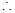

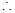
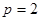 故所求抛物线方程为
故所求抛物线方程为 ---------4分
---------4分
(Ⅱ)设 ,
,
过抛物线上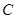 、
、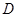 两点的切线方程分别是
两点的切线方程分别是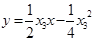 ,
,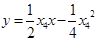
 两条切线的交点
两条切线的交点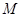 的坐标为
的坐标为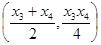
设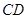 的直线方程为
的直线方程为 ,代入
,代入 得
得
 故
故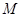 的坐标为
的坐标为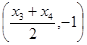 点
点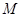 的轨迹为
的轨迹为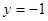 ---------------8分
---------------8分

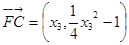
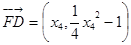
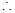

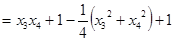

而
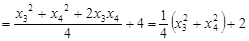
故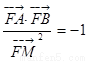 -----------------------------------12分
-----------------------------------12分


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
6
| ||
| 5 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
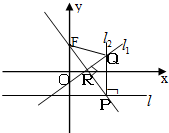 (2012•威海二模)如图,在平面直角坐标系xoy中,设点F(0,p)(p>0),直线l:y=-p,点p在直线l上移动,R是线段PF与x轴的交点,过R、P分别作直线l1、l2,使l1⊥PF,l2⊥l l1∩l2=Q.
(2012•威海二模)如图,在平面直角坐标系xoy中,设点F(0,p)(p>0),直线l:y=-p,点p在直线l上移动,R是线段PF与x轴的交点,过R、P分别作直线l1、l2,使l1⊥PF,l2⊥l l1∩l2=Q.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,A、B为半椭圆
如图,A、B为半椭圆| y2 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |

| k |
| 2 |
| k |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com