
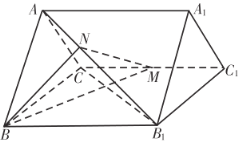
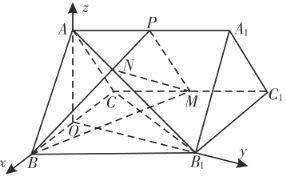
【题目】已知三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)条件①:直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;
;
条件②:![]() 为锐角,三棱锥
为锐角,三棱锥![]() 的体积为
的体积为![]() .
.
在以上两个条件中任选一个,补充在下面的问题中,并解决该问题:
若平面![]() 平面
平面![]() ,______,求平面
,______,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】(1)见解析;(2)见解析.
【解析】
(1)延长![]() 交
交![]() 于点,连接
于点,连接![]() ,证明出点
,证明出点![]() 为
为![]() 的中点,进而证明出四边形
的中点,进而证明出四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,再利用线面平行的判定定理可证明出
,再利用线面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)选条件①,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明出
,证明出![]() 平面
平面![]() ,由直线
,由直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,可求得
,可求得![]() ,并证明出
,并证明出![]() ,然后以点
,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,利用空间向量法能计算出平面
轴建立空间直角坐标系,利用空间向量法能计算出平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
选条件②,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明出
,证明出![]() 平面
平面![]() ,由三棱锥
,由三棱锥![]() 的体积为
的体积为![]() 计算出
计算出![]() ,可得出
,可得出![]() ,并证明出
,并证明出![]() ,然后以点
,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,利用空间向量法能计算出平面
轴建立空间直角坐标系,利用空间向量法能计算出平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(1)延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() 为
为![]() 的中点,
的中点,
因为![]() 为
为![]() 的中点,
的中点,![]() 且
且![]() ,
,
所以![]() 且
且![]() ,则四边形
,则四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ;
;

(2)选择条件①,解答过程如下:
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 为直角三角形,所以
为直角三角形,所以![]() ,且
,且![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 为
为![]() 与平面
与平面![]() 所成的角,
所成的角,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() .
.
如图,以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以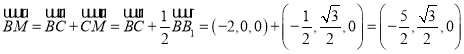 ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则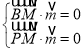 ,即
,即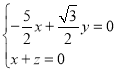 ,
,
取![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
因为平面![]() 轴,所以平面
轴,所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以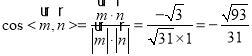 ,
,
所以平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值
所成的锐二面角的余弦值![]() ;
;
选择条件②,解答过程如下:
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 为直角三角形,所以
为直角三角形,所以![]() ,且
,且![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 为三棱锥
为三棱锥![]() 的高,
的高,
因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为![]() 为锐角,所以
为锐角,所以![]() ,
,
因为![]() ,所以
,所以![]() 为等边三角形,所以
为等边三角形,所以![]() .
.
如图,以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以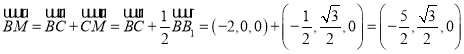 ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则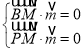 ,即
,即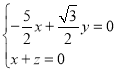 ,
,
取![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
因为平面![]() 轴,所以平面
轴,所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以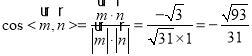 ,
,
所以平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值
所成的锐二面角的余弦值![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,N为
,N为![]() 的中点.
的中点.
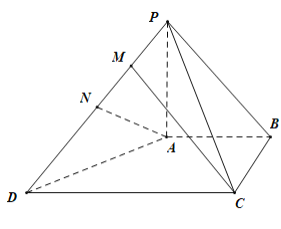
(1)求证:![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
(3)在线段![]() 上是否存在一点M,使得直线
上是否存在一点M,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)若存在x0∈R,f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A,B两点的横坐标是函数f(x)的不动点,且A,B两点关于直线y=kx+![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明每天从家步行去学校,有两条路线可以选择,第一条路线,需走天桥,不用等红灯,平均用时910秒;第二条路线,要经过两个红绿灯路口,如图,A处为小明家,D处为学校,走路段![]() 需240秒,在B处有一红绿灯,红灯时长120秒,绿灯时长30秒,走路段
需240秒,在B处有一红绿灯,红灯时长120秒,绿灯时长30秒,走路段![]() 需450秒,在C处也有一红绿灯,红灯时长100秒,绿灯时长50秒,走路段
需450秒,在C处也有一红绿灯,红灯时长100秒,绿灯时长50秒,走路段![]() 需200秒.小明进行了60天的试验,每天都选择第二条路线,并记录了在B处等待红灯的时长,经统计,60天中有48天在B处遇到红灯,根据记录的48天等待红灯时长的数据绘制了下面的频率分布直方图.已知B处和C处的红灯亮起的时刻恰好始终保持相同,且红绿灯之间切换无时间间隔.
需200秒.小明进行了60天的试验,每天都选择第二条路线,并记录了在B处等待红灯的时长,经统计,60天中有48天在B处遇到红灯,根据记录的48天等待红灯时长的数据绘制了下面的频率分布直方图.已知B处和C处的红灯亮起的时刻恰好始终保持相同,且红绿灯之间切换无时间间隔.

(1)若小明选择第二条路线,设当小明到达B处的时刻为B处红灯亮起后的第x秒(![]() )时,小明在B处等待红灯的时长为y秒,求y关于x的函数的解析式;
)时,小明在B处等待红灯的时长为y秒,求y关于x的函数的解析式;
(2)若小明选择第二条路线,请估计小明在B处遇到红灯的概率,并问小明是否可能在B处和C处都遇到红灯;
(3)若取区间中点作为该区间对应的等待红灯的时长,以这两条路线的平均用时作为决策依据,小明应选择哪一条路线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图中有一个信号源和五个接收器.接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号.若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所得六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com