
【题目】已知函数![]() .
.
(1)求证:对任意实数![]() ,都有
,都有![]() ;
;
(2)若![]() ,是否存在整数
,是否存在整数![]() ,使得在
,使得在![]() 上,恒有
上,恒有![]() 成立?若存在,请求出
成立?若存在,请求出![]() 的最大值;若不存在,请说明理由.(
的最大值;若不存在,请说明理由.(![]() )
)
【答案】(1)见证明;(2)见解析
【解析】
(1)利用导数求得![]()
![]() ,令
,令![]() ,再利用导数即可求得
,再利用导数即可求得![]() ,问题得证。
,问题得证。
(2)整理![]() 得:
得:![]() ,令:
,令:![]() ,由
,由![]() 得
得![]() ,对
,对![]() 是否大于
是否大于![]() 分类, 当
分类, 当![]() 时,即
时,即![]() 时,利用导数即可证得
时,利用导数即可证得![]() ,当
,当![]() 时,利用导数即可求得
时,利用导数即可求得![]() ,要使不等式
,要使不等式![]() 恒成立转化成
恒成立转化成![]() 成立,令
成立,令![]() ,利用导数即可求得
,利用导数即可求得![]() ,
,![]() ,即可求得
,即可求得![]() ,问题得解。
,问题得解。
解:(1)证明:由已知易得![]() ,所以
,所以![]()
令![]() 得:
得:![]()
显然,![]() 时,
时,![]() <0,函数f(x)单调递减;
<0,函数f(x)单调递减;
![]() 时,
时,![]() >0,函数f(x)单调递增
>0,函数f(x)单调递增
所以![]()
![]()
令![]() ,则由
,则由![]() 得
得![]()
![]() 时,
时,![]() >0,函数t(
>0,函数t(![]() )单调递增;
)单调递增;
![]() 时,
时,![]() <0,函数t(
<0,函数t(![]() )单调递减
)单调递减
所以![]() ,即结论成立.
,即结论成立.
(2)由题设化简可得![]()
令![]() ,所以
,所以![]()
由![]() =0得
=0得![]()
①若![]() ,即
,即![]() 时,在
时,在![]() 上,有
上,有![]() ,故函数
,故函数![]() 单调递增
单调递增
所以![]()
②若![]() ,即
,即![]() 时,
时,
在![]() 上,有
上,有![]() ,故函数
,故函数![]() 在
在![]() 上单调递减
上单调递减
在![]() 上,有
上,有![]() .故函数
.故函数![]() 在
在![]() 上单调递增
上单调递增
所以,在![]() 上,
上,![]()
故欲使![]() ,只需
,只需![]() 即可
即可
令![]()
由![]() 得
得![]()
所以,![]() 时,
时,![]() ,即
,即![]() 单调递减
单调递减
又![]()
![]()
故![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | |
直径/mm | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(I)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行判定(
,并根据以下不等式进行判定(![]() 表示相应事件的概率):①
表示相应事件的概率):①![]() ;②
;②![]() ;③
;③![]() .判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁.试判断设备
.判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁.试判断设备![]() 的性能等级.
的性能等级.
(Ⅱ)将直径尺寸在![]() 之外的零件认定为是“次品”,将直径尺寸在
之外的零件认定为是“次品”,将直径尺寸在![]() 之外的零件认定为“突变品”.从样本的“次品”中随意抽取两件,求至少有一件“突变品”的概率.
之外的零件认定为“突变品”.从样本的“次品”中随意抽取两件,求至少有一件“突变品”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂![]() ,
,![]() 两条生产线生产同款产品,若产品按照一、二、三等级分类,则每件可分别获利10元、8元、6元,现从
两条生产线生产同款产品,若产品按照一、二、三等级分类,则每件可分别获利10元、8元、6元,现从![]() ,
,![]() 生产线的产品中各随机抽取100件进行检测,结果统计如下图:
生产线的产品中各随机抽取100件进行检测,结果统计如下图:
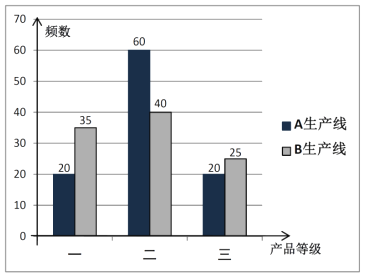
(1)根据已知数据,判断是否有99%的把握认为一等级产品与生产线有关?
(2)分别计算两条生产线抽样产品获利的方差,以此作为判断依据,说明哪条生产线的获利更稳定?
(3)估计该厂产量为2000件产品时的利润以及一等级产品的利润.
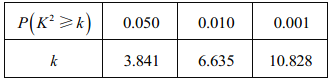
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为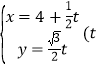 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x2+1)﹣e﹣|x|(e为自然对数的底数),则不等式f(2x+1)>f(x)的解集是( )
A. (﹣1,1)B. (﹣∞,﹣1)∪(1,+∞)
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中华人民共和国国旗是五星红旗,旗面左上方缀着的五颗黄色五角星,四颗小五角星环拱于大星之右,象征中国共产党领导下的革命人民大团结和人民对党的衷心拥护.五角星可通过正五边形连接对角线得到,且它具有一些优美的特征,如![]() 且等于黄金分割比
且等于黄金分割比![]() ,现从正五边形A1B1C1D1E1内随机取一点,则此点取自正五边形A2B2C2D2E2内部的概率为()
,现从正五边形A1B1C1D1E1内随机取一点,则此点取自正五边形A2B2C2D2E2内部的概率为()
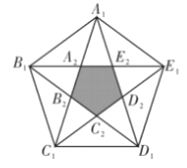
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝,![]() )的函数解析式.
)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
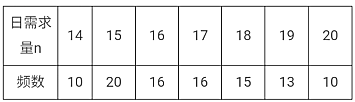
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进![]() 枝玫瑰花,
枝玫瑰花,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列,数学期望及方差;
的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 是曲线
是曲线![]() 截直线
截直线![]() 所得线段的中点,求
所得线段的中点,求![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com