
下列四个命题中不正确的是 ( )
A.若动点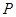 与定点
与定点 、
、 连线
连线 、
、 的斜率之积为定值
的斜率之积为定值 ,则动点
,则动点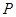 的轨迹为双曲线的一部分
的轨迹为双曲线的一部分
B.设 ,常数
,常数 ,定义运算“
,定义运算“ ”:
”: ,若
,若 ,则动点
,则动点 的轨迹是抛物线的一部分
的轨迹是抛物线的一部分
C.已知两圆 、圆
、圆 ,动圆
,动圆 与圆
与圆 外切、与圆
外切、与圆 内切,则动圆的圆心
内切,则动圆的圆心 的轨迹是椭圆
的轨迹是椭圆
D.已知 ,椭圆过
,椭圆过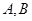 两点且以
两点且以 为其一个焦点,则椭圆的另一个焦点的轨迹为双曲线
为其一个焦点,则椭圆的另一个焦点的轨迹为双曲线
D
【解析】
试题分析:对A,一般地,由题设知直线PA与PB的斜率存在且均不为零kPA?kPB=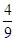 ,整理得,点P的轨迹方程为
,整理得,点P的轨迹方程为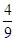 x2-y2=
x2-y2=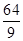 (x≠±4),即动点
(x≠±4),即动点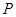 的轨迹为双曲线的一部分,A正确;
的轨迹为双曲线的一部分,A正确;
B:∵m*n=(m+n)2-(m-n)2,∴
,设P(x,y),则y=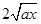 ,即y2=4ax(x≥0,y≥0),即动点动点
,即y2=4ax(x≥0,y≥0),即动点动点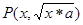 的轨迹是抛物线的一部分,B正确;
的轨迹是抛物线的一部分,B正确;
C:由题意可知,动圆M与定圆A相外切与定圆B相内切
∴MA=r+1,MB=5-r
∴MA+MB=6>AB=2
∴动圆圆心M的轨迹是以A,B为焦点的椭圆,C正确;
D设此椭圆的另一焦点的坐标D (x,y),
∵椭圆过A、B两点,则 CA+DA=CB+DB,
∴15+DA=13+DB,∴DB-DA=2<AB,
∴椭圆的另一焦点的轨迹是以A、B为焦点的双曲线一支,D错误
故选 D
考点:本题主要考查圆、椭圆、双曲线的定义及标准方程。
点评:本题考查知识点覆盖面广,解答难度大,能较全面地考查学生对圆锥曲线问题的掌握情况。


科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 4 |
| A、函数f(x)是周期函数 | ||
B、函数f(x)的图象关于点(-
| ||
| C、函数f(x)是偶函数 | ||
D、函数f(x)的图象关于直线x=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A.半圆所对的圆心角是π rad
B.周角的大小等于2π
C.1弧度的圆心角所对的弧长等于该圆的半径
D.长度等于半径的弦所对的圆心角的大小是1弧度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com