
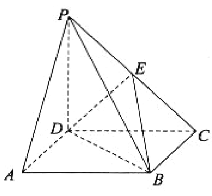
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,三棱锥![]() 的体积是18,求
的体积是18,求![]() 点到平面
点到平面![]() 的距离.
的距离.
【答案】(1)见解析 ;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)推导出BC⊥PD,BD⊥BC,由此能证明BC⊥平面PBD.(2)连结AC,交BD于O,连结OE,由PA∥平面BDE,得OE∥PA,由此能求出![]() .(3)B到平面PCD的距离d=
.(3)B到平面PCD的距离d=
3![]() ,设PD=a,则
,设PD=a,则![]() =
=![]() ,由三棱锥P﹣BDE的体积是18,求出PD=a=6,设点D到平面PAB的距离为h,由VP﹣ABD=VD﹣PAB,能求出D点到平面PAB的距离.
,由三棱锥P﹣BDE的体积是18,求出PD=a=6,设点D到平面PAB的距离为h,由VP﹣ABD=VD﹣PAB,能求出D点到平面PAB的距离.
(1)∵在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PD⊥平面ABCD,
∴BC⊥PD,∵AD=BD=6,AB=6![]() ,BC=AD,∴BD2+BC2=CD2,∴BD⊥BC,
,BC=AD,∴BD2+BC2=CD2,∴BD⊥BC,
∵PD∩BD=D,∴BC⊥平面PBD.
(2)连结AC交BD于O,连结OE,则O是AC的中点,

∵PA∥平面BDE,∴OE∥PA,∴E是PC的中点,∴![]() =
=![]() .
.
(3)B到平面PCD的距离d=![]() =3
=3![]() ,设PD=a,则
,设PD=a,则![]() =
=![]()
![]() =
=![]() ,∵三棱锥P﹣BDE的体积是18,∴VP﹣BDE=VB﹣PDE=
,∵三棱锥P﹣BDE的体积是18,∴VP﹣BDE=VB﹣PDE=![]() =
=![]() =18,解得PD=a=6,设点D到平面PAB的距离为h,
=18,解得PD=a=6,设点D到平面PAB的距离为h,
∵PD⊥平面ABCD,AD=BD=6,AB=6![]() ,
,
∴PA=PB=![]() =6
=6![]() ,
,
∴![]() =18
=18![]() ,
,
![]() =
=![]() =18,
=18,
∵VP﹣ABD=VD﹣PAB,∴![]() ,
,
∴h=![]() =
=![]() =2
=2![]() .∴D点到平面PAB的距离为2
.∴D点到平面PAB的距离为2![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
①对于任意一个圆O,其“优美函数”有无数个;
②函数f(x)=ln(![]() )可以是某个圆的“优美函数”;
)可以是某个圆的“优美函数”;
③函数y=1+sinx可以同时是无数个圆的“优美函数”;
④函数y=2x+1可以同时是无数个圆的“优美函数”;
⑤函数y=f(x)是“优美函数”的充要条件为函数y=f(x)的图象是中心对称图形.
其中正确的命题是_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,椭圆C过点![]() ,两个焦点为
,两个焦点为![]() ,
,![]() ,E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,直线EF的斜率为
,E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,直线EF的斜率为![]() ,直线l与椭圆C相切于点A,斜率为
,直线l与椭圆C相切于点A,斜率为![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的一个焦点是
的一个焦点是![]() ,且
,且![]()
(1)求双曲线![]() 的方程
的方程
(2)设经过焦点![]() 的直线
的直线![]() 的一个法向量为
的一个法向量为![]() ,当直线
,当直线![]() 与双曲线
与双曲线![]() 的右支相交于不同的两点
的右支相交于不同的两点![]() 时,求实数
时,求实数![]() 的取值范围
的取值范围
(3)设(2)中直线![]() 与双曲线
与双曲线![]() 的右支相交于
的右支相交于![]() 两点,问是否存在实数
两点,问是否存在实数![]() ,使得
,使得![]() 为锐角?若存在,请求出
为锐角?若存在,请求出![]() 的范围;若不存在,请说明理由
的范围;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com