
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 为整数,当
为整数,当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最大值(其中
的最大值(其中![]() 为
为![]() 的导函数).
的导函数).
【答案】(Ⅰ)![]() 的单调区间递增区间为
的单调区间递增区间为![]() ,递减区间为
,递减区间为![]() ; (Ⅱ)整数
; (Ⅱ)整数![]() 的最大值为
的最大值为![]() .
.
【解析】试题分析:(Ⅰ)求出原函数的导函数,由f'(ln2)=1求导a值,再由f(ln2)=﹣ln2求得b值,代入原函数的导函数,再由导函数的符号与原函数单调性间的关系确定原函数的单调区间;
(Ⅱ)将条件转化为![]() ,当
,当![]() 时恒成立. 令
时恒成立. 令![]() ,利用导数求最小值得答案.
,利用导数求最小值得答案.
试题解析:
(Ⅰ)![]() ,由已知得
,由已知得![]() ,故
,故![]() ,解得
,解得![]()
又![]() ,得
,得![]() ,解得
,解得![]() .
.
![]() ,所以
,所以![]()
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]()
所以![]() 的单调区间递增区间为
的单调区间递增区间为![]() ,递减区间为
,递减区间为![]() .
.
(Ⅱ)法一.由已知![]() ,及
,及![]() 整理得
整理得
![]() ,当
,当![]() 时恒成立
时恒成立
令![]() ,
, 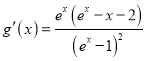 .
.
当![]() 时,
时, ![]() ;
;
由(Ⅰ)知![]() 在
在![]() 上为增函数,
上为增函数,
又![]() .
.
所以存在![]() 使得
使得![]() ,此时
,此时![]()
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]()
所以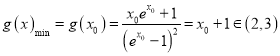 .
.
故整数![]() 的最大值为
的最大值为![]() .
.
法二.由已知![]() ,及
,及![]() 整理得,
整理得, ![]()
令![]() ,
, ![]()
![]() 得,
得, ![]() .
.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,
, ![]() 在
在![]() 上为减函数,
上为减函数,
![]() .
.
![]() ,
, ![]() 为增函数。
为增函数。![]()
![]()
![]() 为减函数。
为减函数。![]()
由已知 ![]() .
.
令![]() ,
, ![]() ,
, ![]() 在
在![]() 上为增函数.
上为增函数.
又![]() ,
,
故整数![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=|1﹣![]() |
|
(1)求满足f(x)=2的x值;
(2)是否存在实数a,b,且0<a<b<1,使得函数y=f(x)在区间[a,b]上的值域为[a,2b],若存在,求出a,b的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kx2+2x(k为实常数)为奇函数,函数g(x)=af(x)﹣1(a>0且a≠1).
(Ⅰ)求k的值;
(Ⅱ)求g(x)在[﹣1,2]上的最大值;
(Ⅲ)当a=![]() 时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
时,g(x)≤t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,它们在
,它们在![]() 轴右侧有两个交点
轴右侧有两个交点![]() 、
、![]() ,满足
,满足![]() .将直线
.将直线![]() 左侧的椭圆部分(含
左侧的椭圆部分(含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() ,直线
,直线![]() 右侧的双曲线部分(不含
右侧的双曲线部分(不含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() .以
.以![]() 为端点作一条射线,分别交
为端点作一条射线,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() (点
(点![]() 在第一象限),设此时
在第一象限),设此时![]() .
.
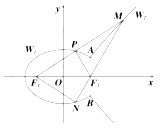
(1)求![]() 的方程;
的方程;
(2)证明: ![]() ,并探索直线
,并探索直线![]() 与
与![]() 斜率之间的关系;
斜率之间的关系;
(3)设直线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.
求(1)三棱锥A﹣CDE的全面积;
(2)点D到平面ACE的距离.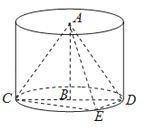
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2017年“双![]() ”,“双
”,“双![]() ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共![]() 个,生产一个汤碗需
个,生产一个汤碗需![]() 分钟,生产一个花瓶需
分钟,生产一个花瓶需![]() 分钟,生产一个茶杯需
分钟,生产一个茶杯需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润![]() 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润![]() 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润![]() 元.
元.
(1)使用每天生产的汤碗个数![]() 与花瓶个数
与花瓶个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4![]() 4:坐标系与参数方程
4:坐标系与参数方程
在直角坐标系![]() 中,已知直线l1:
中,已知直线l1: ![]() (
(![]() ,
, ![]() ),抛物线C:
),抛物线C: 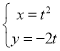 (t为参数).以原点
(t为参数).以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com