
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与曲线
处的切线与曲线![]() 相切,求
相切,求![]() 的值;
的值;
(2)当![]() 时,函数
时,函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象的下方,求
的图象的下方,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 恰有2个不相等的零点,求实数
恰有2个不相等的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)先写出曲线![]() 在
在![]() 处的切线方程,再设切线与
处的切线方程,再设切线与![]() 相切的切点为
相切的切点为![]() ,
,![]() ,
,![]() ,
,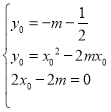 ,可解出
,可解出![]() .
.
(2)由题知任意![]() ,
,![]() ,
,![]() 恒成立,
恒成立,![]() 恒成立,可得出
恒成立,可得出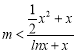 ,令
,令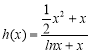 ,
,![]() ,
,![]() ,只需
,只需![]() 小于
小于![]() 的最小值即可.
的最小值即可.
(3)![]() ,
,![]() 分五种情况当
分五种情况当![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 时,讨论函数
时,讨论函数![]() 单调性,分析
单调性,分析![]() 的零点,进而得出
的零点,进而得出![]() 的取值范围.
的取值范围.
解:(1)![]() ,
,
函数![]() 的导数为
的导数为![]() ,
,
函数![]() 在
在![]() 处的切线的斜率为
处的切线的斜率为![]() ,
,
函数![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() .
.
由函数![]() 在
在![]() 处的切线与函数
处的切线与函数![]() 相切,
相切,
联立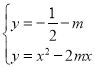 ,得
,得![]() .
.
所以![]() ,得
,得![]() .
.
(2)设函数![]()
![]() ,
,
所以![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
由题意![]() ,
,
所以![]() .
.
②当![]() 时,当
时,当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
由题意![]() ,
,
即![]() .
.
又因为![]() ,
,![]() 不成立.
不成立.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.
(3)![]()
![]() .
.
①当![]() 时,若
时,若![]() ,
,![]() ,
,![]() 单调递增;
单调递增;
若![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
若![]() ,
,![]() ,
,![]() 单调递增.
单调递增.
所以![]() 的极大值为
的极大值为![]()
![]() ,
,
所以函数![]() 的图象与
的图象与![]() 轴至多有一个交点.
轴至多有一个交点.
④当![]() 时,若
时,若![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
若![]() ,
,![]() ,
,![]() 单调递增.
单调递增.
所以![]() .
.
(1)当![]() ,即
,即![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴至多有一个交点.
轴至多有一个交点.
(2)当![]() ,即
,即![]() 时,
时,
![]()
![]() .
.
令![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
所以当![]() 时,
时,![]() ,
,
所以![]() ,
,
所以存在![]() ,
,![]() .
.
![]()
![]()
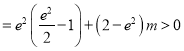 ,
,
所以存在![]() ,
,![]() .
.
(3)当![]() 时,
时,![]() 只有一个零点,
只有一个零点,
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左、右顶点分别为A,B,左焦点为F,O为原点,点P为椭圆C上不同于A、B的任一点,若直线PA与PB的斜率之积为
)的左、右顶点分别为A,B,左焦点为F,O为原点,点P为椭圆C上不同于A、B的任一点,若直线PA与PB的斜率之积为![]() ,且椭圆C经过点
,且椭圆C经过点![]() .
.
(1)求椭圆C的方程;
(2)若P点不在坐标轴上,直线PA,PB交y轴于M,N两点,若直线OT与过点M,N的圆G相切.切点为T,问切线长![]() 是否为定值,若是,求出定值,若不是,请说明理由.
是否为定值,若是,求出定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张坐标纸上一已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为
的轨迹为![]() .
.
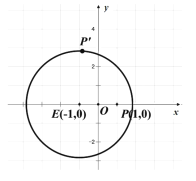
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于两个不同的点
交于两个不同的点![]() ,且直线
,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:

表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:
![]()
如果把5根算筹以适当的方式全部放入 下面的表格中,那么可以表示的三位数的个数为( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图a是某市参加2012年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为![]() 、
、![]() 、…、
、…、![]() [如
[如![]() 表示身高(单位:cm)在
表示身高(单位:cm)在![]() 内的学生人数].图b是统计图a中身高在一定范围内学生人数的一个算法流程图.现要统计身高在
内的学生人数].图b是统计图a中身高在一定范围内学生人数的一个算法流程图.现要统计身高在![]() (含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )
(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com