练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    为平行四边形的一条对角线，　　　．

     

    【答案】

    【解析】

    试题分析：根据向量加法的平行四边形法则有，所以.

    考点：向量的加法和减法.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知l，a，b为不同直线，α，β为不同平面，有下列说法：
    ①若直线l与平面α不平行，α内不存在与l平行的直线；
    ②若平面α∥平面β，直线a?α，直线b?β，则直线a∥b；
    ③平面内的一条直线与平面外的一条直线是异面直线；
    ④a⊥α，a⊥b则b∥α；
    ⑤两组对边都相等的四边形是平面图形；
    ⑥α∥β，l⊥α，则l⊥β；
    其中正确的有
    ⑥
    ⑥
    （填序号）

    查看答案和解析>>

    科目：高中数学 来源：全优设计必修二数学苏教版 苏教版 题型：044

    下列各命题是对还是错？

    ①棱柱的侧面都是平行四边形；

    ②棱锥的侧面为三角形，且所有侧面都有一个共同的公共点；

    ③棱台的侧面有的是平行四边形，有的是梯形；

    ④棱台的侧棱所在直线均相交于同一点；

    ⑤将直角梯形绕着它的一条腰所在的直线旋转一周所得的几何体叫做圆台；

    ⑥圆台的母线是互相平行的线段；

    ⑦多面体至少有四个面；

    ⑧旋转体只有圆柱、圆锥、圆台和球等这四类几何体；

    ⑨球有无数条对称轴；

    ⑩棱锥和棱台及棱柱中，均有五面体．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知大西北某荒漠上两点相距2千米，现准备在荒漠上围垦出一片以为一条对角线的平行四边形区域建农艺园．按照规划，围墙总长为8千米．

    （1）试求四边形另两个顶点的轨迹方程；

    （2）该荒漠上有一条直线型小溪刚好通过点，且与成角．现要对整条小溪进行改造，因考虑到小溪可能被农艺园围进的部分今后重新设计改造，因此对该部分暂不改造．问暂不改造的部分有多长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    下列语句是命题并且为真命题的是
    ①x2-5x+6＝0
    ②对x＝4，2x＜0
    ③垂直于同一条直线的两条直线必平行吗
    ④矩形难道不是平行四边形吗
    ⑤一个数不是合数就是质数
    ⑥求证：若x∈R，方程x2-x+1＝0无实根


    1. A.
      ④⑤⑥
    2. B.
      ④⑥
    3. C.
      ⑥
    4. D.
      ④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

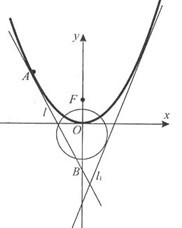    （本题满分15分）如图，已知直线与抛物线和圆都相切，是的焦点.

    （1）求与的值；

    （2）设是上的一动点，以为切点作抛物线的切线，直线交轴于点，以为邻边作平行四边形，证明：点在一条定直线上；

    （3）在（2）的条件下，记点所在的定直线为，直线与轴交点为，连接交抛物线于两点，求的面积的取值范围.

    22。（本题满分15分）已知函数．

    （1）求函数的图像在点处的切线方程；

    （2）若，且对任意恒成立，求的最大值；

    （3）当时，证明．

    查看答案和解析>>

    同步练习册答案