
����Ŀ���̲���һ���������£�
һֻ�����IJ�����y���¶�x�йأ����ռ���7��۲��������±����Խ���y��x֮��Ļع鷽�̣�
�¶� x/�� | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
������y/�� | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
ijͬѧ����ͼ�μ������о���ʱ��������ɢ��ͼ����ͼ��ʾ��������������������������ع�ϵ�� �������еĺ���֪ʶ������������ֲ���ijһ��ָ��������![]() �ĸ�����
�ĸ�����![]() ��
��![]() �Ǵ����IJ����������ǽ��������µļ�����
�Ǵ����IJ����������ǽ��������µļ�����
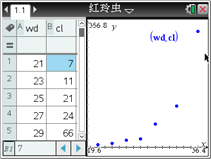
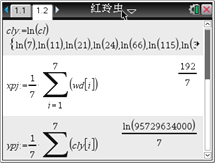
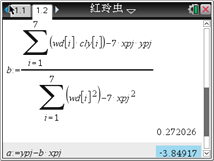
�������ϼ����������Եõ������IJ�����y���¶�x�Ļع鷽��Ϊ__________������ȷ��0.0001�� ����ʾ��![]() ���ô�����ת��Ϊ���Թ�ϵ��
���ô�����ת��Ϊ���Թ�ϵ��
 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���о�ijҩƷ����Ч��ѡȡ������־Ը�߽����ٴ����飮����־Ը�ߵ�����ѹ���ݣ���λ��kPa���ķ�������Ϊ[12��13����[13��14����[14��15����[15��16����[16��17]�����䰴�����ҵ�˳��ֱ���Ϊ��һ�飬�ڶ��飬���������飮��ͼ�Ǹ������������Ƴɵ�Ƶ�ʷֲ�ֱ��ͼ����֪��һ����ڶ��鹲��20�ˣ���������û����Ч����6�ˣ��������������Ч������Ϊ�� �� 
A.6
B.8
C.12
D.18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���������ѧ���μ�ѧУ��֯�ġ���ѧ���ˡ���ս���� ÿ�˾������ִ�����ᣬ���ҽ�����һ�ֲ�����ʱ���еڶ��ִ���.����ƽʱ���飬�ס��ҡ���������ѧ��ÿ�ֹ��صĸ��ʷֱ�Ϊ![]() ����������ѧ��ÿ�ֹ������Ӱ��.
����������ѧ��ÿ�ֹ������Ӱ��.
��1����ס��ҡ���������ѧ���������صĸ��ʣ�
��2����![]() Ϊ�ס��ҡ���������ѧ���й��ص����������������
Ϊ�ס��ҡ���������ѧ���й��ص����������������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��վ�Ӵ����ڼ�����շ����������ֻ��û��������ȡ![]() �����е��飬���ܷ��û�������ֳ�
�����е��飬���ܷ��û�������ֳ�![]() �飺
�飺 ![]() ��
�� ![]() ������
������ ![]() ���������õ�����Ƶ�ʷֲ�ֱ��ͼ��
���������õ�����Ƶ�ʷֲ�ֱ��ͼ��

������![]() ��ֵ��
��ֵ��
���Ӵ����ڼ�����շ����������ֻ��û��������ȡһ�ˣ��������������![]() ��ĸ��ʣ�
��ĸ��ʣ�
�����ƴ����ڼ�����շ����������ֻ��û���ƽ�����䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���о���ѧ�����Ա���ɼ������������̡��Ķ�����4�������Ĺ�ϵ����������52����ѧ�����õ�ͳ���������1����4�������Ա��й����Ŀ��������ı����ǣ� ��
��1
�ɼ� | ������ | ���� | �ܼ� |
�� | 6 | 14 | 20 |
Ů | 10 | 22 | 32 |
�ܼ� | 16 | 36 | 52 |
��2
���� | �� | �� | �ܼ� |
�� | 4 | 16 | 20 |
Ů | 12 | 20 | 32 |
�ܼ� | 16 | 36 | 52 |
��3
���� | ƫ�� | ���� | �ܼ� |
�� | 8 | 12 | 20 |
Ů | 8 | 24 | 32 |
�ܼ� | 16 | 36 | 52 |
��4
�Ķ��� | �ḻ | ���ḻ | �ܼ� |
�� | 14 | 6 | 20 |
Ů | 2 | 30 | 32 |
�ܼ� | 16 | 36 | 52 |
A.�ɼ�
B.����
C.����
D.�Ķ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�У�ABCDΪ���Σ�ƽ��PAD��ƽ��ABCD�� 
��1����֤��AB��PD��
��2������BPC=90�㣬PB= ![]() ��PC=2����ABΪ��ֵʱ������P��ABCD�����������ʱƽ��BPC��ƽ��DPC�нǵ�����ֵ��
��PC=2����ABΪ��ֵʱ������P��ABCD�����������ʱƽ��BPC��ƽ��DPC�нǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f0��x��= ![]() ��x��0������fn��x��Ϊfn��1��x���ĵ�����n��N* ��
��x��0������fn��x��Ϊfn��1��x���ĵ�����n��N* ��
��1����2f1�� ![]() ��+
��+ ![]() f2��
f2�� ![]() ����ֵ��
����ֵ��
��2��֤����������n��N* �� ��ʽ|nfn��1�� ![]() ��+
��+ ![]() fn��
fn�� ![]() ��|=
��|= ![]() ��������
��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʵ����һ����¶ȣ���λ���棩��ʱ��t����λ��h���ı仯�������㺯����ϵ��
f��t��=10�� ![]() ��t��[0��24��
��t��[0��24��
��1����ʵ������һ�������²
��2����Ҫ��ʵ�����¶Ȳ�����11�棬�����Ķ�ʱ��ʵ������Ҫ���£�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com