
(本题满分16分)已知函数 (其中
(其中 为常数,
为常数, )为偶函数.
)为偶函数.
(1) 求 的值;
的值;
(2) 用定义证明函数 在
在 上是单调减函数;
上是单调减函数;
(3) 如果 ,求实数
,求实数 的取值范围.
的取值范围.
(1)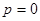 ;(2)见解析;(3)
;(2)见解析;(3)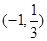
【解析】
试题分析:(1) 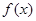 是偶函数有
是偶函数有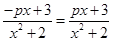 即
即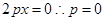 .…………4分
.…………4分
(2)由(1)  . 设
. 设 , ………………6分
, ………………6分
则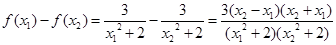 . ……………………8分
. ……………………8分

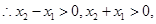
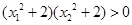 .
.

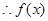 在
在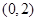 上是单调减函数. ……………………10分
上是单调减函数. ……………………10分
(3)由(2)得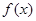 在
在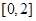 上为减函数,又
上为减函数,又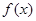 是偶函数,所以
是偶函数,所以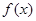 在
在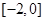 上为单调增函数.
……………………………………………12分
上为单调增函数.
……………………………………………12分
不等式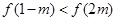 即
即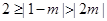 ,4>
,4> .
.
解得 . 所以实数
. 所以实数 的取值范围是
的取值范围是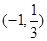 .…………………16分
.…………………16分
说明(3)如果是分情况讨论,知道分类给2分.并做对一部分则再给2分.
考点:函数的奇偶性;函数的单调性;利用函数的奇偶性和单调性解不等式。
点评:解这类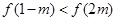 不等式,关键是利用函数的奇偶性和它在定义域内的单调性,去掉“f”符号,转化为代数不等式组求解,但要特别注意函数定义域的作用。
不等式,关键是利用函数的奇偶性和它在定义域内的单调性,去掉“f”符号,转化为代数不等式组求解,但要特别注意函数定义域的作用。


 考前必练系列答案
考前必练系列答案科目:高中数学 来源:2010-2011年江苏省淮安市楚州中学高二上学期期末考试数学试卷 题型:解答题
(本题满分16分)
已知函数 ,且对任意
,且对任意 ,有
,有 .
.
(1)求 ;
;
(2)已知 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数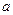 的取值范围.
的取值范围.
(3)讨论函数 的零点个数?(提示
的零点个数?(提示 :
: )
)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三10月阶段性测试理科数学试卷(解析版) 题型:解答题
(本题满分16分)已知函数 为实常数).
为实常数).
(I)当 时,求函数
时,求函数 在
在 上的最小值;
上的最小值;
(Ⅱ)若方程 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(Ⅲ)证明:
(参考数据: )
)
查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二下期中理科数学试卷(解析版) 题型:解答题
(本题满分16分) 已知椭圆 :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 的左、右焦点,若椭圆
的左、右焦点,若椭圆 的焦距为2.
的焦距为2.
⑴求椭圆 的方程;
的方程;
⑵设 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分16分)已知函数 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 。
。
(Ⅰ)求 及
及 的值;
的值;
(Ⅱ)求函数 在
在 上的解析式;
上的解析式;
(Ⅲ)若关于 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:江苏省2009-2010学年高二第二学期期末考试 题型:解答题
本题满分16分)已知圆内接四边形ABCD的边长分别为AB = 2,BC = 6,CD = DA = 4 ;求四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com