Question

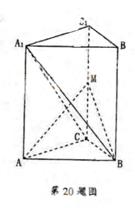
（12分）如图，直三棱住

为侧棱上一点，。

（1）求证：平面；

（2）求二面角的大小；

（3）求点到平面的距离。

Answer 1

解析：证明：（Ⅰ）在直三棱柱ABC－A₁B₁C₁中，易知面

ACC₁A₁⊥面ABC，

∵∠ACB=90°，∴BC⊥面ACC₁A₁， ………2分

∵面ACC₁A₁，∴BC⊥AM

∵，且，∴ AM^平面 ……4分

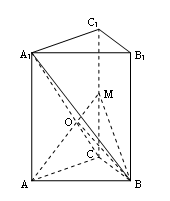
解：（Ⅱ）设AM与A₁C的交点为O，连结BO，由（1）可知

AM ^ OB，且AM ^ OC，

所以∠BOC为二面角B－AM－C的平面角，……6分

在Rt△ACM和Rt△A₁AC中，∠OAC+∠ACO=90°，∴∠AA₁C=∠MAC

∴Rt△ACM∽Rt△A₁AC，∴    

∴

∴在Rt△ACM中，

 ∵，∴

∴在Rt△BCO中，tan

∴，故所求二面角的大小为45°   …… 8分

(Ⅲ)设点C到平面ABM的距离为h，易知，

可得      ……9分

∵                     

∴，

∴

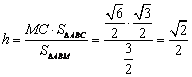
∴点C到平面ABM的距离为 ……12分        

解法二：（1）同解法一 ……………4分

（Ⅱ）如图以C为原点,CA，CB， CC₁所在直线分别

为x轴,y轴,z轴,建立空间直角坐标系，

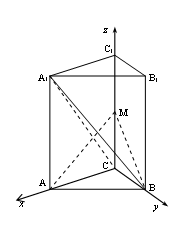
则，设

∵，∴

即，故，

所以    ……6分

设向量为平面AMB的法向量，则

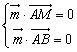，则 即 ，

令x=1，则平面AMB的一个法向量为，显然向量是平面AMC的一个法向量，

易知，与所夹的角等于二面角B－AM－C的大小，故所求二面角的大小为45°．

……8分

(Ⅲ)向量在法向量上的投影的长即为所求距离，

∵  

∴点C到平面ABM的距离为       ……12分