
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设函数![]() ,其中
,其中![]() .证明:
.证明:![]() 的图象在
的图象在![]() 图象的下方.
图象的下方.
【答案】(1) ![]() .
.
(2) ![]() .
.
(3)证明见解析.
【解析】分析:(Ⅰ)求出函数的导数,计算![]() 和
和![]() 的值,点斜式求出切线方程即可.
的值,点斜式求出切线方程即可.
(Ⅱ)设![]() ,并求导.将问题转化为在区间
,并求导.将问题转化为在区间![]() 上,
上,![]() 恒成立,或者
恒成立,或者![]() 恒成立,通过特殊值
恒成立,通过特殊值![]() ,且
,且![]() ,确定
,确定![]() 恒成立,通过参数分离,求得实数
恒成立,通过参数分离,求得实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,将问题转化为证明
,将问题转化为证明![]() ,利用函数的导数确定函数最小值
,利用函数的导数确定函数最小值![]() 在区间
在区间![]() ,并证明
,并证明![]() . 即
. 即![]() 的图象在
的图象在![]() 图象的下方.
图象的下方.
详解:解:(Ⅰ)求导,得![]() ,
,
又因为![]()
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(Ⅱ)设函数![]() ,
,
求导,得![]() ,
,
因为函数![]() 在区间
在区间![]() 上为单调函数,
上为单调函数,
所以在区间![]() 上,
上,![]() 恒成立,或者
恒成立,或者![]() 恒成立,
恒成立,
又因为![]() ,且
,且![]() ,
,
所以在区间![]() ,只能是
,只能是![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
又因为函数![]() 在在区间
在在区间![]() 上单调递减,
上单调递减,![]() ,
,
所以![]() .
.
(Ⅲ)证明:设![]() .
.
求导,得![]() .
.
设![]() ,则
,则![]() (其中
(其中![]() ).
).
所以当![]() 时,
时,![]() (即
(即![]() )为增函数.
)为增函数.
又因为![]() ,
,
所以,存在唯一的![]() ,使得
,使得![]()
且![]() 与
与![]() 在区间
在区间![]() 上的情况如下:
上的情况如下:
|
|
|
|
| - | 0 | + |
| ↘ |
| ↗ |
所以,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]()
![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,即
,即![]() 的图象在
的图象在![]() 图象的下方.
图象的下方.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某中学一名数学老师对全班50名学生某次考试成绩分男女生进行统计(满分150分),其中120分(含120分)以上为优秀,绘制了如图所示的两个频率分布直方图:

(1)根据以上两个直方图完成下面的![]() 列联表:
列联表:
性别 成绩 | 优秀 | 不优秀 | 总计 |
男生 | |||
女生 | |||
总计 |
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
附:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球队在4次不同比赛中的得分情况如下:
甲队 | 88 | 91 | 92 | 96 |
乙队 | 89 | 93 | 9▓ | 92 |
乙队记录中有一个数字模糊(即表中阴影部分),无法确认,假设这个数字具有随机性,并用![]() 表示.
表示.
(Ⅰ)在4次比赛中,求乙队平均得分超过甲队平均得分的概率;
(Ⅱ)当![]() 时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2个比赛得分之差的绝对值为
时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2个比赛得分之差的绝对值为![]() ,求随机变量
,求随机变量![]() 的分布列;
的分布列;
(Ⅲ)如果乙队得分数据的方差不小于甲队得分数据的方差,写出![]() 的取值集合.(结论不要求证明)
的取值集合.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)当k=1时,求函数f(x)的单调区间;
(2)当 ![]() 时,求函数f(x)在[0,k]上的最大值M.
时,求函数f(x)在[0,k]上的最大值M.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现行的个税法修正案规定:个税免征额由原来的2000元提高到3500元,并给出了新的个人所得税税率表:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3% |
超过1500元至4500元的部分 | 10% |
超过4500元至9000元的部分 | 20% |
超过9000元至35000元的部分 | 25% |
…… | … |
例如某人的月工资收入为5000元,那么他应纳个人所得税为:![]() (元).
(元).
(Ⅰ)若甲的月工资收入为6000元,求甲应纳的个人收的税;
(Ⅱ)设乙的月工资收入为![]() 元,应纳个人所得税为
元,应纳个人所得税为![]() 元,求
元,求![]() 关于
关于![]() 的函数;
的函数;
(Ⅲ)若丙某月应纳的个人所得税为1000元,给出丙的月工资收入.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
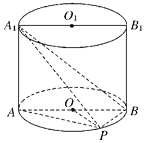
【题目】如图,已知点P在圆柱OO1的底面⊙O上,![]() 分别为⊙O、⊙O1的直径,且
分别为⊙O、⊙O1的直径,且![]() 平面
平面![]() .
.
(1)求证:![]() ;
;
(2)若圆柱![]() 的体积
的体积![]() ,
,
①求三棱锥A1﹣APB的体积.
②在线段AP上是否存在一点M,使异面直线OM与![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①用 刻画回归效果,当
刻画回归效果,当![]() 越大时,模型的拟合效果越差,反之则越好;②归纳推理是由特殊到一般的推理,而演绎推移则是由一般到特殊的推理;③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”;④设有一个回归方程
越大时,模型的拟合效果越差,反之则越好;②归纳推理是由特殊到一般的推理,而演绎推移则是由一般到特殊的推理;③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”;④设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位;⑤线性回归方程
平均增加5个单位;⑤线性回归方程![]() 必过点
必过点![]() .其中错误的个数有( )
.其中错误的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com