
【题目】已知定义在R上的函数![]() 在[0,7]上有1和6两个零点,且函数
在[0,7]上有1和6两个零点,且函数![]() 与函数
与函数![]() 都是偶函数,则
都是偶函数,则![]() 在[0,2019]上的零点至少有( )个
在[0,2019]上的零点至少有( )个
A.404B.406C.808D.812
【答案】C
【解析】
根据y=f(x+2)与y=f(x+7)都是偶函数,得到函数f(x)=f(10+x),得到函数是周期函数,利用函数的周期性即可得到函数零点的个数,即可求解.
由题意,函数y=f(x+2)与y=f(x+7)都是偶函数,
可得函数f(x)关于x=2和x=7对称,即![]()
所以![]() ,可得
,可得![]() ,所以10是函数f(x)的一个周期,
,所以10是函数f(x)的一个周期,
又由定义域为R的函数y=f(x)在[0,7]上有1和6两个零点,可知3和8也是函数的零点,
可得f(x)=0的根为10n+1或10n+3或10n+6或10n+8的形式,
所以0≤10n+1≤2019,解得-0.1≤n≤201.8,共201个,
由0≤10n+3≤2019,解得-0.3≤n≤201.6,共201个,
由0≤10n+6≤2019,解得-0.6≤n≤201.3,共201个,
由0≤10n+8≤2019,解得-0.8≤n≤201.1,共201个,
故函数y=f(x)在[0,2019]上的零点个数为808个,
故选:C.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】在所有棱长都相等的三棱锥![]() 中,D,E,F分别是AB,BC,CA的中点,下列四个命题:
中,D,E,F分别是AB,BC,CA的中点,下列四个命题:
(1)![]() 平面PDF;(2)
平面PDF;(2)![]() 平面
平面![]() ;
;
(3)平面![]() 平面
平面![]() ;(4)平面
;(4)平面![]() 平面
平面![]() .
.
其中正确命题的序号为________.
A.(2)(3)B.(1)(3)C.(2)(4)D.(1)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .
.
(1)若点![]() 也是顶点为原点的抛物线
也是顶点为原点的抛物线![]() 的焦点,求抛物线
的焦点,求抛物线![]() 的方程;
的方程;
(2)当![]() 与
与![]() 轴垂直时,求直线
轴垂直时,求直线![]() 的方程;
的方程;
(3)设![]() 为坐标原点,证明:
为坐标原点,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已定义![]() ,已知函数
,已知函数![]() 的定义域都是
的定义域都是![]() ,则下列四个命题中为真命题的是_________.(写出所有真命题的序号)
,则下列四个命题中为真命题的是_________.(写出所有真命题的序号)
① 若![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数.
为奇函数.
② 若![]() 都是偶函数,则函数
都是偶函数,则函数![]() 为偶函数.
为偶函数.
③ 若![]() 都是增函数,则函数
都是增函数,则函数![]() 为增函数.
为增函数.
④ 若![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数.
为减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是空气质量的一个重要指标,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35μg/m3以下空气质量为一级,在35μg/m3~75μg/m3之间空气质量为二级,在75μg/m3以上空气质量为超标.如图是某市2019年12月1日到10日PM2.5日均值(单位:μg/m3)的统计数据,则下列叙述不正确的是( )
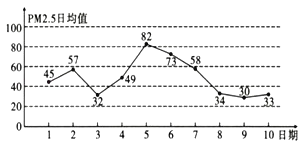
A.这10天中,12月5日的空气质量超标
B.这10天中有5天空气质量为二级
C.从5日到10日,PM2.5日均值逐渐降低
D.这10天的PM2.5日均值的中位数是47
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com