
【题目】在△ABC中,角A,B,C的对边分别是a,b,c已知ccosB+(b-2a)cosC=0
(1)求角C的大小
(2)若c=2,a+b=ab,求△ABC的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)由题意首先利用正弦定理边化角,据此求得![]() ,则角C的大小是
,则角C的大小是![]() ;
;
(2)由题意结合余弦定理可得![]() ,然后利用面积公式可求得△ABC的面积为
,然后利用面积公式可求得△ABC的面积为![]() .
.
试题解析:
(1)∵ccosB+(b-2a)cosC=0,
由正弦定理化简可得:sinCcosB+sinBcosC-2sinAcosC=0,即sinA=2sinAcosC,
∵0<A<π, ∴sinA≠0. ∴cosC=![]() . ∵0<C<π, ∴C=
. ∵0<C<π, ∴C=![]() .
.
(2)由(1)可知:C=![]() .
.
∵c=2,a+b=ab,即a2b2=a2+b2+2ab.
由余弦定理cosC=![]() =
=![]() ,
,
∴ab=(ab)2-2ab-c2.
可得:ab=4.
那么:△ABC的面积S=![]() absinC=
absinC=![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
, ![]() 垂直于
垂直于![]() 和
和![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中点.
的中点.
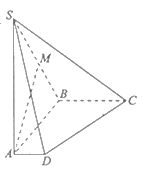
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的二面角的余弦值;
所成的二面角的余弦值;
(Ⅲ)设点![]() 是直线
是直线![]() 上的动点,
上的动点, ![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为![]() ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为![]() .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为![]() ,求
,求![]() 的分布列及数学期望E
的分布列及数学期望E![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 上任意一点,且点
上任意一点,且点![]() 到椭圆
到椭圆![]() 的一个焦点的最大距离等于
的一个焦点的最大距离等于![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同两点
相交于不同两点![]() ,设
,设![]() 为椭圆上一点,是否存在整数
为椭圆上一点,是否存在整数![]() ,使得
,使得![]() (其中
(其中![]() 为坐标原点)?若存在,试求整数
为坐标原点)?若存在,试求整数![]() 的所有取值;若不存在,请说明理由.
的所有取值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
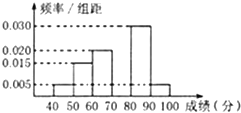
【题目】某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如图频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]).
(1)求成绩在[70,80)的频率和[70,80)这组在频率分布直方图中的纵坐标a的值;
(2)求这次考试平均分的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,并制成下面的![]() 列联表:
列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 6 | 26 |
经常使用手机 | 10 | 14 | 24 |
合计 | 30 | 20 | 50 |
(1)判断是否有![]() 的把握认为经常使用手机对学习成绩有影响?
的把握认为经常使用手机对学习成绩有影响?
(2)从这50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数学题,甲、乙独立解出此题的概率分别为![]() ,且
,且![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“学习师徒”,记
,则此二人适合结为学习上互帮互助的“学习师徒”,记![]() 为两人中解出此题的人数,若
为两人中解出此题的人数,若![]() 的数学期望
的数学期望![]() ,问两人是否适合结为“学习师徒”?
,问两人是否适合结为“学习师徒”?
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式及数据: 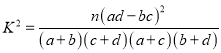 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com