
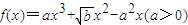 ,存在实数x1,x2满足下列条件:①x1<x2;②f′(x1)=f′(x2)=0;③|x1|+|x2|=2
,存在实数x1,x2满足下列条件:①x1<x2;②f′(x1)=f′(x2)=0;③|x1|+|x2|=2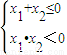 ,又x1<x2,可知x1<0,x2>0,
,又x1<x2,可知x1<0,x2>0,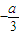 ≤-1,解得0<a≤3,从而命题得证.
≤-1,解得0<a≤3,从而命题得证.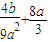 =4,整理得b=9a2-6a3,a∈(0,3],
=4,整理得b=9a2-6a3,a∈(0,3],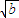 x1-a2,由(1)知
x1-a2,由(1)知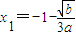 代入h(x1)表达式
代入h(x1)表达式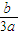 ,由(2)知b=9a2-6a3,于是h(x1)=a2且0<a≤3,所以0<a2≤12a恒成立.故|h(x1)|≤12a得证.
,由(2)知b=9a2-6a3,于是h(x1)=a2且0<a≤3,所以0<a2≤12a恒成立.故|h(x1)|≤12a得证.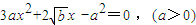 有两个根,由韦达定理得,
有两个根,由韦达定理得,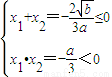 又x1<x2,可知x1<0,x2>0,再由|x1|+|x2|=2可得,x1≤-1,0<x2≤1,所以x1•x2≤-1,
又x1<x2,可知x1<0,x2>0,再由|x1|+|x2|=2可得,x1≤-1,0<x2≤1,所以x1•x2≤-1,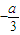 ≤-1,解得0<a≤3,从而命题得证.
≤-1,解得0<a≤3,从而命题得证.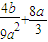 =4,整理得b=9a2-6a3,a∈(0,3],
=4,整理得b=9a2-6a3,a∈(0,3], x1-a2,由(1)知
x1-a2,由(1)知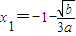 代入h(x1)表达式,即h(x1)=-a2+3a-
代入h(x1)表达式,即h(x1)=-a2+3a- ,由(2)知b=9a2-6a3,于是h(x1)=a2且0<a≤3,所以0<a2≤9,即0<a2≤12恒成立.
,由(2)知b=9a2-6a3,于是h(x1)=a2且0<a≤3,所以0<a2≤9,即0<a2≤12恒成立.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2006年浙江省杭州市高考数学二模试卷(理科)(解析版) 题型:解答题
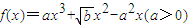 ,存在实数x1,x2满足下列条件:①x1<x2;②f′(x1)=f′(x2)=0;③|x1|+|x2|=2
,存在实数x1,x2满足下列条件:①x1<x2;②f′(x1)=f′(x2)=0;③|x1|+|x2|=2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com