
【题目】已知函数![]() (
(![]() R).
R).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若对任意实数![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
试题(1)求函数的单调区间,实质上就是解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(2)函数的最大值一般与函数的单调性联系在一起,本题中
得减区间;(2)函数的最大值一般与函数的单调性联系在一起,本题中![]() ,其单调性要对
,其单调性要对![]() 进行分类,
进行分类,![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,不合题意,故有
上单调递减,不合题意,故有![]() ,按极值点
,按极值点![]() 与0的大小分类研究单调性有最大值.
与0的大小分类研究单调性有最大值.
试题解析:(1)当![]() 时,
时,![]() ,
,
则![]() ,
,
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,
,
∴函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由题意![]() ,
,
(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,此时,不存在实
上单调递减,此时,不存在实
数![]() ,使得当
,使得当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() .
.
(2)当![]() 时,令
时,令![]() ,有
,有![]() ,
,![]() ,
,
①当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,显然符合题意.
上单调递增,显然符合题意.
②当![]() 即
即![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 处取得极大值,且
处取得极大值,且![]() ,
,
要使对任意实数![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,
,
只需![]() ,解得
,解得![]() ,又
,又![]() ,
,
所以此时实数![]() 的取值范围是
的取值范围是![]() .
.
③当![]() 即
即![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减,要存在实数
上单调递减,要存在实数![]() ,使得当
,使得当![]() 时,
时,
函数![]() 的最大值为
的最大值为![]() ,需
,需![]() ,
,
代入化简得![]() ,①
,①
令![]() ,因为
,因为![]() 恒成立,
恒成立,
故恒有![]() ,所以
,所以![]() 时,①式恒成立,
时,①式恒成立,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
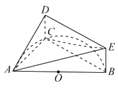
(1)证明:平面ADE⊥平面ACD;
(2)当C点为半圆的中点时,求二面角D﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店销售某种商品,为了解该商品的月销量![]() (单位:千件)与月售价
(单位:千件)与月售价![]() (单位:元/件)之间的关系,对近几年的月销售量
(单位:元/件)之间的关系,对近几年的月销售量![]() 和月销售价
和月销售价![]() 数据进行了统计分析,得到了下面的散点图.
数据进行了统计分析,得到了下面的散点图.
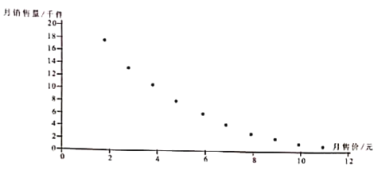
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为月销量
哪一个更适宜作为月销量![]() 关于月销售价
关于月销售价![]() 的回归方程类型?(给出判断即可,不需说明理由),并根据判断结果及表中数据,建立
的回归方程类型?(给出判断即可,不需说明理由),并根据判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)利用(1)中的结果回答问题:已知该商品的月销售额为![]() (单位:千元),当月销售量为何值时,商品的月销售额预报值最大?(月销售额=月销售量×当月售价)
(单位:千元),当月销售量为何值时,商品的月销售额预报值最大?(月销售额=月销售量×当月售价)
参考公式、参考数据及说明:
①对一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为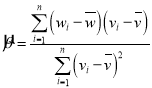 ,
,![]() .
.
②参考数据:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 | -143.25 | -27.54 |
表中![]() ,
,![]() .
.
③计算时,所有的小数都精确到0.01,如![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由单位正方形组成的无限格阵的每个单位正方形内都写有一个整数.若每个方格内的整数等于其上方和左方与其相邻的两个方格内的整数之和,且存在一行![]() ,其中,所有方格内的数都是正整数.记
,其中,所有方格内的数都是正整数.记![]() 下面一行为
下面一行为![]() ,
,![]() 下面一行为
下面一行为![]() ,证明:对于每个正整数
,证明:对于每个正整数![]() ,
,![]() 上不能有
上不能有![]() 个方格内的整数都是0.
个方格内的整数都是0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com