练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对于代数式（x+1）n+1+（x+2）2n－1（n∈N*）能被___________整除.

    A.2x+3                                                             B.x2+3x+3

    C.x2+2x+3                                                       D.x2+5x+5

    解析：取n=1知能被x2+3x+3整除.

    答案：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知点B1（1，y1），B2（2，y2），…，Bn（n，yn）（n∈N*）在直线y=
    1
    2
    x+1    上，点A1（x1，0），A2（x2，0），A3（x3，0），…，An（xn，0）顺次为x轴上的点，其中x1=a（0＜a＜1），对于任意n∈N*，点An，Bn，An+1构成以∠Bn为顶角的等腰三角形，设△AnBnAn+1的面积为Sn，
    （1）证明：数列{yn}是等差数列；
    （2）求S2n-1（用a和n的代数式表示）；
    （3）设数列{
    1
    S2n-1S2n
    }    前n项和为Tn，判断Tn与
    8n
    3n+4
    （n∈N*）的大小，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点B1（1，y1），B2（2，y2），…，Bn（n，yn）（n∈N*）在直线y=
    12
    x+1    上，点A1（x1，0），A2（x2，0），A3（x3，0）…An（xn，0）顺次为x轴上的点，其中x1=a（0＜a＜1），对于任意n∈N*，点An，Bn，An+1构成以∠Bn为顶点的等腰三角形，设△AnBnAn+1的面积为Sn．
    （1）证明：数列{yn}是等差数列；
    （2）求S2n-1（用n和a的代数式表示）．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省深圳市高级中学高三（上）第一次月考数学试卷（理科）（解析版） 题型：解答题

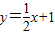    已知点B1（1，y1），B2（2，y2），…，Bn（n，yn）（n∈N*）在直线上，点A1（x1，0），A2（x2，0），A3（x3，0），…，An（xn，0）顺次为x轴上的点，其中x1=a（0＜a＜1），对于任意n∈N*，点An，Bn，An+1构成以∠Bn为顶角的等腰三角形，设△AnBnAn+1的面积为Sn，
    （1）证明：数列{yn}是等差数列；
    （2）求S2n-1（用a和n的代数式表示）；
    （3）设数列前n项和为Tn，判断Tn与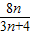（n∈N*）的大小，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源：2010年广东省高考数学冲刺预测试卷04（理科）（解析版） 题型：解答题

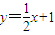    已知点B1（1，y1），B2（2，y2），…，Bn（n，yn）（n∈N*）在直线上，点A1（x1，0），A2（x2，0），A3（x3，0），…，An（xn，0）顺次为x轴上的点，其中x1=a（0＜a＜1），对于任意n∈N*，点An，Bn，An+1构成以∠Bn为顶角的等腰三角形，设△AnBnAn+1的面积为Sn，
    （1）证明：数列{yn}是等差数列；
    （2）求S2n-1（用a和n的代数式表示）；
    （3）设数列前n项和为Tn，判断Tn与（n∈N*）的大小，并证明你的结论．

    查看答案和解析>>

    同步练习册答案