
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离减去
的距离减去![]() 到直线
到直线![]() 的距离等于1.
的距离等于1.
(1)求曲线![]() 的方程;
的方程;
(2)若直线 ![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求证:直线
两点,求证:直线![]() 与直线
与直线![]() 的倾斜角互补.
的倾斜角互补.
科目:高中数学 来源: 题型:
【题目】现有一长为100码,宽为80码,球门宽为8码的矩形足球运动场地,如图所示,其中![]() 是足球场地边线所在的直线,球门
是足球场地边线所在的直线,球门![]() 处于所在直线的正中间位置,足球运动员(将其看做点
处于所在直线的正中间位置,足球运动员(将其看做点![]() )在运动场上观察球门的角
)在运动场上观察球门的角![]() 称为视角.
称为视角.
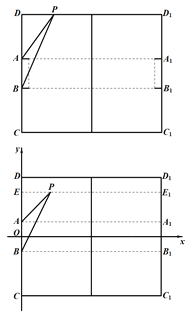
(1)当运动员带球沿着边线![]() 奔跑时,设
奔跑时,设![]() 到底线的距离为
到底线的距离为![]() 码,试求当
码,试求当![]() 为何值时
为何值时![]() 最大;
最大;
(2)理论研究和实践经验表明:张角![]() 越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以
越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以![]() 的中点为原点建立如图所示的直角坐标系,求在球场区域
的中点为原点建立如图所示的直角坐标系,求在球场区域![]() 内射门到球门
内射门到球门![]() 的最佳射门点的轨迹.
的最佳射门点的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.

青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一列非零向量![]() 满足:
满足:![]() ,
,![]() .
.
(1)写出数列![]() 的通项公式;
的通项公式;
(2)求出向量![]() 与
与![]() 的夹角
的夹角![]() ,并将
,并将![]() 中所有与
中所有与![]() 平行的向量取出来,按原来的顺序排成一列,组成新的数列
平行的向量取出来,按原来的顺序排成一列,组成新的数列![]() ,
,![]() ,
,![]() 为坐标原点,求点列
为坐标原点,求点列![]() 的坐标;
的坐标;
(3)令![]() (
(![]() ),求
),求![]() 的极限点位置.
的极限点位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月,台风“山竹”在我国多个省市登陆,造成直接经济损失达52亿元.某青年志愿者组织调查了某地区的50个农户在该次台风中造成的直接经济损失,将收集的数据分成五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元),得到如图所示的频率分布直方图.
(单位:元),得到如图所示的频率分布直方图.
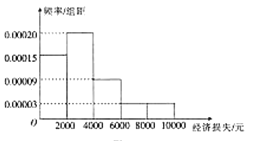
(1)试根据频率分布直方图估计该地区每个农户的平均损失(同一组中的数据用该组区间的中点值代表);
(2)台风后该青年志愿者与当地政府向社会发出倡议,为该地区的农户捐款帮扶,现从这50户并且损失超过4000元的农户中随机抽取2户进行重点帮扶,设抽出损失超过8000元的农户数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是圆
是圆![]() 上的任意一点,
上的任意一点,![]() 是过点
是过点![]() 且与
且与![]() 轴垂直的直线,
轴垂直的直线,![]() 是直线
是直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .当点
.当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .判定直线
.判定直线![]() 的斜率是否依次构成等差数列?并说明理由.
的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,如图
的中点,如图![]() 将
将![]() 沿
沿![]() 折到
折到![]() 的位置,使
的位置,使![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,如图2.
,如图2.
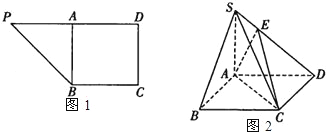
![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() 求二面角
求二面角![]() 的正切值;
的正切值;
![]() 在线段
在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com