
【题目】(1)阅读以下案例,利用此案例的想法化简![]() .
.
案例:考察恒等式![]() 左右两边
左右两边![]() 的系数.
的系数.
因为右边![]() ,
,
所以,右边![]() 的系数为
的系数为![]() ,
,
而左边![]() 的系数为
的系数为![]() ,
,
所以![]() =
=![]() .
.
(2)求证:![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)考查恒等式(1+x)7=(1+x)3(x+1)4左右两边x3的系数可得;
(2)根据![]() ,考查恒等式(1+x)2n=(1+x)n(x+1)n左右两边xn的系数.考查恒等式(1+x)2n﹣1=(1+x)n﹣1(x+1)n左右两边xn﹣1的系数,可得等式成立.
,考查恒等式(1+x)2n=(1+x)n(x+1)n左右两边xn的系数.考查恒等式(1+x)2n﹣1=(1+x)n﹣1(x+1)n左右两边xn﹣1的系数,可得等式成立.
(1)考查恒等式(1+x)7=(1+x)3(x+1)4左右两边x3的系数,
因为右边(1+x)3(x+1)4=(![]() +
+![]() x+
x+![]() x2+
x2+![]() x3)(
x3)(![]() x4+
x4+![]() x3+
x3+![]() x2+
x2+![]() x+
x+![]() ),
),
所以,右边x3的系数为![]() =
=![]()
而左边x3的系数为:![]() ,所以
,所以![]() .
.
(2)∵![]() ,
,
![]()
![]()
![]() .
.
考查恒等式(1+x)2n=(1+x)n(x+1)n左右两边xn的系数.
因为右边xn的系数为![]() =
=![]() ,而左边的xn的系数为
,而左边的xn的系数为![]() .
.
所以![]() ,同理可求得
,同理可求得![]()
考查恒等式(1+x)2n﹣1=(1+x)n﹣1(x+1)n左右两边xn﹣1的系数,
因为右边(1+x)n﹣1(x+1)n=(![]() +
+![]() x+…+
x+…+![]() xn﹣1)(
xn﹣1)(![]() xn+
xn+![]() xn﹣1+…+
xn﹣1+…+![]() ),
),
所以,右边的xn﹣1的系数为![]() =
=![]() ,
,
而左边的xn﹣1的系数为![]() ,所以
,所以![]() =
=![]() ,
,
![]() ﹣
﹣![]() =
=![]() +2n
+2n![]() +
+![]() ﹣
﹣![]()
=2n![]() +
+![]() =n(
=n(![]() +
+![]() )+
)+![]() =n(
=n(![]() +
+![]() )+
)+![]()
=n![]() +
+![]() =(n+1)
=(n+1)![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() ,点G,H分别为边
,点G,H分别为边![]() ,
,![]() 的中点,点M是线段
的中点,点M是线段![]() 上的动点.
上的动点.
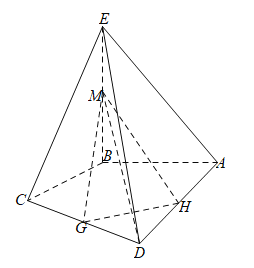
(1)求证:![]() ;
;
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求点C到平面
的体积最大时,求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 的中点,
的中点,![]() 在侧面
在侧面![]() 上,有下列四个命题:
上,有下列四个命题:
①若![]() ,则
,则![]() 面积的最小值为
面积的最小值为![]() ;
;
②平面![]() 内存在与
内存在与![]() 平行的直线;
平行的直线;
③过![]() 作平面
作平面![]() ,使得棱
,使得棱![]() ,
,![]() ,
,![]() 在平面
在平面![]() 的正投影的长度相等,则这样的平面
的正投影的长度相等,则这样的平面![]() 有4个;
有4个;
④过![]() 作面
作面![]() 与面
与面![]() 平行,则正方体
平行,则正方体![]() 在面
在面![]() 的正投影面积为
的正投影面积为![]() .
.
则上述四个命题中,真命题的个数为( )
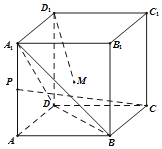
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在著名的汉诺塔问题中,有三根高度相同的柱子和一些大小及颜色各不相同的圆盘,三根柱子分别为起始柱、辅助柱及目标柱.已知起始柱上套有![]() 个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将
个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将![]() 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为
个圆盘从起始柱移动到目标柱上最少需要移动的次数记为![]() ,则
,则![]() ( )
( )

A. 33B. 31C. 17D. 15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 轴,
轴,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求三条曲线
,求三条曲线![]() ,
,![]() ,
,![]() 所围成图形的面积.
所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中,![]() ,且对任意
,且对任意![]() ,
,![]() 成等差数列,其公差为
成等差数列,其公差为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,证明
,证明![]() 成等比数列(
成等比数列(![]() );
);
(3)若对任意![]() ,
,![]() 成等比数列,其公比为
成等比数列,其公比为![]() ,设
,设![]() ,证明数列
,证明数列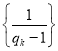 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校针对校食堂饭菜质量开展问卷调查,提供满意与不满意两种回答,调查结果如下表(单位:人):
学生 | 高一 | 高二 | 高三 |
满意 | 500 | 600 | 800 |
不满意 | 300 | 200 | 400 |
(1)求从所有参与调查的人中任选1人是高三学生的概率;
(2)从参与调查的高三学生中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求这两人对校食堂饭菜质量都满意的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com