
【题目】已知等差数列![]() 与等比数列
与等比数列![]() 是非常数的实数列,设
是非常数的实数列,设![]() .
.
(1)请举出一对数列![]() 与
与![]() ,使集合
,使集合![]() 中有三个元素;
中有三个元素;
(2)问集合![]() 中最多有多少个元素?并证明你的结论;
中最多有多少个元素?并证明你的结论;
【答案】(1) ![]() .
.
(2)3个,证明见解析.
【解析】分析:(1)![]() ,则
,则![]() ;(2)不妨设
;(2)不妨设![]() ,由
,由![]() ,令
,令![]() ,原问题转化为
,原问题转化为![]() 关于的方程
关于的方程![]() 最多有多少个解,可以证明当
最多有多少个解,可以证明当![]() 时,方程①最多有
时,方程①最多有![]() 个解:
个解:![]() 时,方程①最多有
时,方程①最多有![]() 个解,从而可得结果.
个解,从而可得结果.
详解:(1)![]() ,则
,则![]()
(2)不妨设![]() ,由
,由![]()
令![]() ,原问题转化为
,原问题转化为![]() 关于的方程
关于的方程
![]() ①
①
最多有多少个解.
下面我们证明:当![]() 时,方程①最多有
时,方程①最多有![]() 个解:
个解:![]() 时,方程①最多有
时,方程①最多有![]() 个解
个解
当![]() 时,考虑函数
时,考虑函数![]() ,则
,则![]()
如果![]() ,则
,则![]() 为单调函数,故方程①最多只有一个解;
为单调函数,故方程①最多只有一个解;
如果![]() ,且不妨设由
,且不妨设由![]() 得
得![]() 由唯一零点
由唯一零点![]() ,于是当
,于是当![]() 时,
时,
![]() 恒大于
恒大于![]() 或恒小于
或恒小于![]() ,当
,当![]() 时,
时,![]() 恒小于
恒小于![]() 或恒大于
或恒大于![]()
这样![]() 在区间
在区间![]() 与
与![]() 上是单调函数,故方程①最多有
上是单调函数,故方程①最多有![]() 个解
个解
当![]() 时,如果
时,如果![]()
如果![]() 为奇数,则方程①变为
为奇数,则方程①变为
![]()
显然方程最多只有一个解,即最多只有一个奇数满足方程①
如果![]() 为偶数,则方程①变为
为偶数,则方程①变为
![]() ,由
,由![]() 的情形,上式最多有
的情形,上式最多有![]() 个解,即满足①的偶数最多有
个解,即满足①的偶数最多有![]() 个
个
这样,最多有![]() 个正数满足方程①
个正数满足方程①
对于![]() ,同理可以证明,方程①最多有
,同理可以证明,方程①最多有![]() 个解.
个解.
综上所述,集合![]() 中的元素个数最多有
中的元素个数最多有![]() 个.
个.
再由(1)可知集合![]() 中的元素个数最多有
中的元素个数最多有![]() 个.
个.


科目:高中数学 来源: 题型:
【题目】汽车的普及给人们的出行带来了诸多方便,但汽车超速行驶也造成了诸多隐患.为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间![]() 中,其频率分布直方图如图所示.
中,其频率分布直方图如图所示.
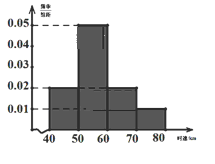
(1)求被抽测的200辆汽车的平均时速.
(2)该路段路况良好,但属于事故高发路段,交警部门对此路段过往车辆限速![]() .对于超速行驶,交警部门对超速车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.罚款情况如下:
.对于超速行驶,交警部门对超速车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.罚款情况如下:
超速情况 | 10%以内 | 10%~20% | 20%~50% | 50%以上 |
罚款情况 | 0元 | 100元 | 150元 | 可以并处吊销驾照 |
①求被抽测的200辆汽车中超速在10%~20%的车辆数.
②该路段车流量比较大,按以前统计该路段每天来往车辆约2000辆.试预估每天的罚款总数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列.在欧洲,这个表叫做帕斯卡三角形,帕斯卡(1623-1662)是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,这是我国数学史上的一个伟大成就.如图所示,在“杨辉三角”中,去除所有为1的项,依次构成数列![]() ,则此数列前135项的和为( )
,则此数列前135项的和为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,E,F分别为线段CD和
中,E,F分别为线段CD和![]() 上的动点,且满足
上的动点,且满足![]() ,则四边形
,则四边形![]() 所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和( )
所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和( )

A. 有最小值![]() B. 有最大值
B. 有最大值![]() C. 为定值3D. 为定值2
C. 为定值3D. 为定值2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某粮食店经销小麦,年销售量为6000千克,每千克小麦进货价为2.8元,销售价为3.4元,全年进货若干次,每次的进货量均为![]() 千克(
千克(![]() ),运费为100元/次,并且全年小麦的总存储费用为
),运费为100元/次,并且全年小麦的总存储费用为![]() 元.
元.
(1)用![]() (千克)表示该粮食店经销小麦的年利润
(千克)表示该粮食店经销小麦的年利润![]() (元);
(元);
(2)每次进货量为多少千克时,能使年利润![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com