
【题目】已知椭圆![]() :
:![]() (
(![]() )的左焦点为
)的左焦点为![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() 与
与![]() 轴垂直,
轴垂直,![]() ,
,![]() 分别为椭圆的右顶点和上顶点,且
分别为椭圆的右顶点和上顶点,且![]() ,且
,且![]() 的面积是
的面积是![]() ,其中
,其中![]() 是坐标原点.
是坐标原点.
(1)求椭圆![]() 的方程.
的方程.
(2)若过点![]() 的直线
的直线![]() ,
,![]() 互相垂直,且分别与椭圆
互相垂直,且分别与椭圆![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() 四点,求四边形
四点,求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 上,且
上,且![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() .
.
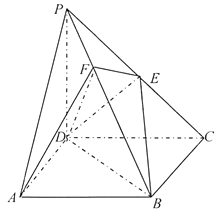
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(Ⅲ)已知![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.
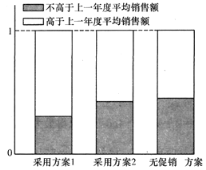
(1)请根据等高条形图提供的信息,为该公司今年选择一套较为有利的促销活动方案(不必说明理由);
(2)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)
(单位:件)![]() 如下表所示:
如下表所示:
售价 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
销量 | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
①请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
②根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
| 52446.95 | 13142 | 122.89 |
| 124650 | ||
(附:相关指数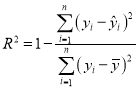 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为4的正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,现将三角形
的中点,现将三角形![]() 沿
沿![]() 翻折成如图2所示的五棱锥
翻折成如图2所示的五棱锥![]() .
.
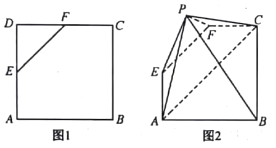
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ(a≠0).
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=asinθ(a≠0).
(1)求圆C的直角坐标方程与直线l的普通方程;
(2)设直线l截圆C的弦长是半径长的![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 与直线
与直线![]() 的两个交点之间的距离;
的两个交点之间的距离;
(2)若曲线![]() 上的点到直线
上的点到直线![]() 距离的最大值为
距离的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本学期学生参加公益劳动的情况,某校从初高中学生中抽取100名学生,收集了他们参加公益劳动时间(单位:小时)的数据,绘制图表的一部分如表.
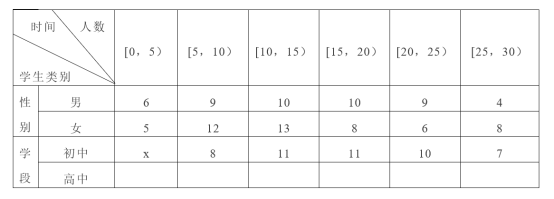
(1)从男生中随机抽取一人,抽到的男生参加公益劳动时间在![]() 的概率:
的概率:
(2)从参加公益劳动时间![]() 的学生中抽取3人进行面谈,记
的学生中抽取3人进行面谈,记![]() 为抽到高中的人数,求
为抽到高中的人数,求![]() 的分布列;
的分布列;
(3)当![]() 时,高中生和初中生相比,那学段学生平均参加公益劳动时间较长.(直接写出结果)
时,高中生和初中生相比,那学段学生平均参加公益劳动时间较长.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com