
已知函数
(I)当 的单调区间;
的单调区间;
(II)若函数 的最小值;
的最小值;
(III)若对任意给定的 ,使得
,使得 的取值范围.
的取值范围.
(I)
(II)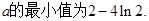
(III)见解析
【解析】(I)当a=1时,解析式是确定的,利用导数大于零求单调增区间,导数小于零求单调减区间即可.
(II)因为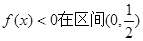 上恒成立不可能,故解本小题的关键是要使函数
上恒成立不可能,故解本小题的关键是要使函数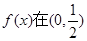 上无零点,只要对任意的
上无零点,只要对任意的 恒成立,即对
恒成立,即对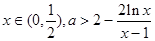 恒成立.然后构造函数
恒成立.然后构造函数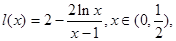 只需要满足
只需要满足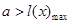 即可.
即可.
(I)当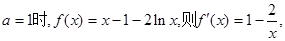 …………1分
…………1分
由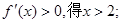 由
由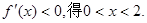
故 …………3分
…………3分
(II)因为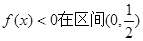 上恒成立不可能,
上恒成立不可能,
故要使函数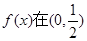 上无零点,只要对任意的
上无零点,只要对任意的 恒成立,
恒成立,
即对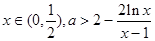 恒成立. …………4分
恒成立. …………4分
令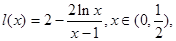
则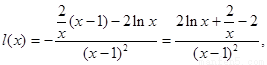 …5分
…5分
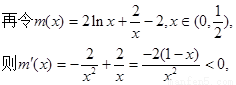
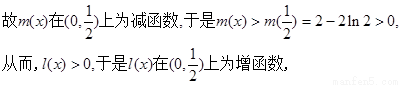
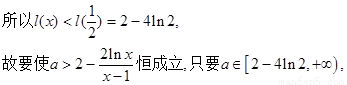
综上,若函数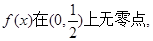
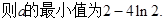 …………6分
…………6分
(III)
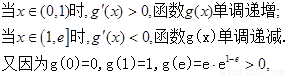
所以,函数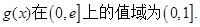 …………7分
…………7分
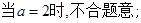

故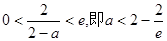 ① …………9分
① …………9分
此时,当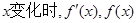 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
— |
0 |
+ |
|
|
|
最小值 |
|
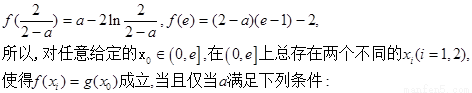
|

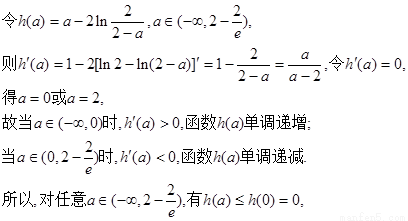
即②对任意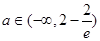 恒成立. …………10分
恒成立. …………10分
由③式解得: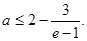 ④
④
综合①④可知,当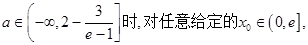
在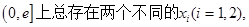
使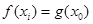 成立.
成立.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:2011-2012学年吉林省延吉市高三数学质量检测理科数学 题型:解答题
(本小题满分12分)已知函数
(I)当 的单调区间和极值;
的单调区间和极值;
(II)若函数 在[1,4]上是减函数,求实数a的取值范围.
在[1,4]上是减函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com