
已知等比数列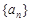 满足
满足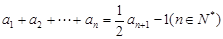 .
.
(1)求数列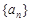 的通项公式;
的通项公式;
(2)在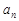 与
与 之间插入
之间插入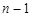 个数连同
个数连同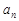 与
与 按原顺序组成一个公差为
按原顺序组成一个公差为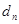 (
(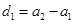 )的等差数列.
)的等差数列.
①设 ,求数列
,求数列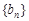 的前
的前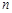 和
和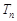 ;
;
②在数列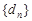 中是否存在三项
中是否存在三项 (其中
(其中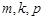 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.
(1)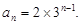 ;(2)①
;(2)①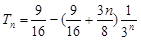 ②不存在.
②不存在.
【解析】
试题分析:(1)要看清问题的实质就是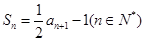 ,那么这就是我们熟悉的问题,利用
,那么这就是我们熟悉的问题,利用 ,转化为
,转化为 和公比
和公比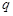 的式子,可解出
的式子,可解出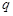 ,再由题目条件得出关于首项的关系式,求出等比数列的首项即可求出通项公式;(2)①由新数列的的首首项和末项及项数可求出公差
,再由题目条件得出关于首项的关系式,求出等比数列的首项即可求出通项公式;(2)①由新数列的的首首项和末项及项数可求出公差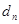 ,根据其表达式的结构特征,再考虑求
,根据其表达式的结构特征,再考虑求 ,本题可用错位相减法;②此类问题,一般先假设存在符合条件的数列,解出来则存在,如果得到矛盾的结果,则假设错误,这样的数列则不存在.
,本题可用错位相减法;②此类问题,一般先假设存在符合条件的数列,解出来则存在,如果得到矛盾的结果,则假设错误,这样的数列则不存在.
试题解析:(1)设数列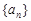 的公比为
的公比为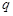 ,由已知可得
,由已知可得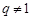 ,
1分
,
1分
由已知,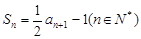 ,所以
,所以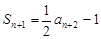 ,
,
两式相减得, ,解得
,解得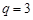 ,
3分
,
3分
又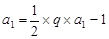 ,解得
,解得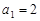 ,
5分
,
5分
故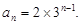 6分
6分
(2)由(1),知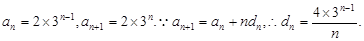 7分
7分
①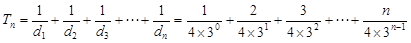 , 8分
, 8分
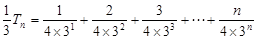 ,
,
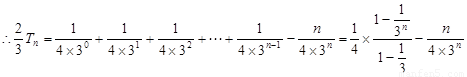 10分
10分
故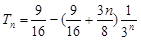 11分
11分
②假设在数列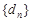 中存在三项
中存在三项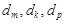 (其中
(其中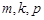 成等差数列)成等比数列,
成等差数列)成等比数列,
则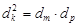 ,即
,即 .
13分
.
13分
因为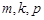 成等差数列,所以
成等差数列,所以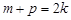 ,(*)代入上式得:
,(*)代入上式得: 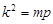 ,(**)
,(**)
由(*),(**),得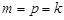 ,这与题设矛盾. 15分
,这与题设矛盾. 15分
所以,在数列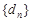 中不存在三项
中不存在三项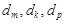 (其中
(其中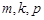 成等差数列)成等比数列. 16分
成等差数列)成等比数列. 16分
考点:等差数列与等比数列、错位相减法.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源:2012-2013学年福建省四地六高三第三次月考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知等比数列 满足
满足 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,
, ,求数列
,求数列 的前
的前 项和
项和 。
。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省名校名师新编“百校联盟”高三第一次调研考试数学理卷 题型:选择题
已知等比数列 满足
满足 ,且
,且 是方程
是方程 的两个实根,则当
的两个实根,则当 等于 ( )
等于 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com