解:(1)∵正方体ABCD-A
1B
1C
1D
1中,DA、DC、DD
1两两互相垂直,
∴以D为原点,分别以DA、DC、DD
1为x、y、z轴,建立如图空间直角坐标系
可得D(0,0,0),A(2,0,0),A
1(2,0,2),C(0,2,0),M(0,1,2),N(0,2,1)
∴向量
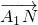
=(-2,2,-1),

=(0,1,-2)
根据空间向量的夹角公式,得cos<
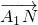
,

>=
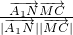
=
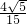
设异面直线A
1N与MC所成角为θ
可得cosθ=|cos<
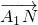
,

>|=
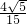
,即异面直线A
1N与MC所成角的余弦值为
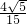
;
(2)由(1)中所建立的坐标系,得
∵P为线段AD上任意一点,
∴设P(x,0,0),其中x∈[0,2]
可得

=(-x,2,1)
∵

=(0,1,-2),
∴

•

=0×(-x)+1×2+(-2)×1=0
由此可得

⊥

,即P为线段AD上任意一点,都有MC⊥PN成立.
分析:(1)以D为原点,分别以DA、DC、DD
1为x、y、z轴,建立如图空间直角坐标系.可得D、A、A
1、C、M、N各点的坐标,从而得到向量
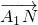
和

的坐标,利用空间向量的夹角公式算出
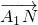
和

夹角的余弦之值,即可得到异面直线A
1N与MC所成角的余弦;
(2)根据(1)所建立的坐标系,设P(x,0,0),从而得到

的坐标,再求出向量

的坐标,从而算得

•

=0,由此可得

⊥

,即得MC⊥PN成立.
点评:本题给出正方体棱的中点,求证直线与直线垂直并求异面直线所成角,着重考查了正方体的性质、空间垂直位置关系的证明和异面直线所成角的求法等知识,属于基础题.

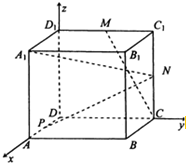
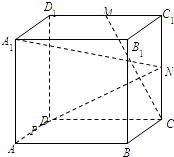 如图,在正方体ABCD-A1B1C1D1中,设AA1=2.M,N分别是C1D1,CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,设AA1=2.M,N分别是C1D1,CC1的中点.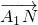 =(-2,2,-1),
=(-2,2,-1), =(0,1,-2)
=(0,1,-2)
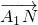 ,
, >=
>=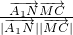 =
=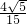
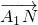 ,
, >|=
>|=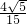 ,即异面直线A1N与MC所成角的余弦值为
,即异面直线A1N与MC所成角的余弦值为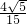 ;
; =(-x,2,1)
=(-x,2,1) =(0,1,-2),
=(0,1,-2), •
• =0×(-x)+1×2+(-2)×1=0
=0×(-x)+1×2+(-2)×1=0 ⊥
⊥ ,即P为线段AD上任意一点,都有MC⊥PN成立.
,即P为线段AD上任意一点,都有MC⊥PN成立.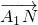 和
和 的坐标,利用空间向量的夹角公式算出
的坐标,利用空间向量的夹角公式算出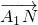 和
和 夹角的余弦之值,即可得到异面直线A1N与MC所成角的余弦;
夹角的余弦之值,即可得到异面直线A1N与MC所成角的余弦; 的坐标,再求出向量
的坐标,再求出向量 的坐标,从而算得
的坐标,从而算得 •
• =0,由此可得
=0,由此可得 ⊥
⊥ ,即得MC⊥PN成立.
,即得MC⊥PN成立.

 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则