
【题目】如图,在四棱锥![]() 中,
中,![]() 是边长为
是边长为![]() 的棱形,且
的棱形,且![]() 分别是
分别是![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)取![]() 中点
中点![]() ,先证明
,先证明![]() 平面
平面![]() ,再证明平面
,再证明平面![]() 平面
平面![]() ,又
,又![]() ,则可得
,则可得![]() 平面
平面![]() (2)先找出
(2)先找出![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,接下来证明
,接下来证明![]() 平面
平面![]() ,所以三棱锥
,所以三棱锥![]() 的高为2.再求
的高为2.再求![]() 的面积
的面积![]() ,利用三棱锥
,利用三棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积相等,即求得点
的体积相等,即求得点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:
(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() .
.
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() 为正角形.
为正角形.
又![]() 为
为![]() 中点,
中点,![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,故
,故![]() 平面
平面![]() .
.
因为![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又![]() ,故
,故![]() 平面
平面![]() .
.
(2)解:因为![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,
,
则![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,且
,且![]() ,所以
,所以![]() .
.
所以![]() ,且
,且![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
所以![]() 平面
平面![]() ,所以三棱锥
,所以三棱锥![]() 的高为2.
的高为2.
于是三棱锥![]() 的体积
的体积![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() ,
,![]() .
.
则在![]() 中,
中,
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,
所以![]() ,于是
,于是![]() 的面积
的面积![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,三棱锥
,三棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积相等,所以
的体积相等,所以![]() ,故
,故![]() .
.



 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:
类舒适型轿车中抽取8辆,经检测它们的得分如下:![]() . 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过
. 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标,现从700袋牛奶中抽取50袋进行检验,利用随机数表抽取样本时,先将700袋牛奶按001,002,…,700进行编号,如果从随机数表第3行第1组开始向右读,最先读到的5袋牛奶的编号是614,593,379,242,203,请你以此方式继续向右读数,随后读出的3袋牛奶的编号是________.(下列摘取了随机数表第1行至第5行)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(2ωx+ ![]() )(其中ω>0),且f(x)的图象在y轴右侧的第一个最高点的横坐标是
)(其中ω>0),且f(x)的图象在y轴右侧的第一个最高点的横坐标是 ![]() .
.
(1)求y=f(x)的最小正周期及对称轴;
(2)若x∈ ![]() ,函数
,函数 ![]() ﹣af(x)+1的最小值为0.求a的值.
﹣af(x)+1的最小值为0.求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2010年至2016年农村居民家庭纯收入![]() (单位:千元)的数据如下表
(单位:千元)的数据如下表
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求![]() 关于
关于![]() 的线性回归方程。
的线性回归方程。
(2)判断![]() 与
与![]() 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2018年农村居民家庭人均纯收入。
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
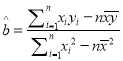 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题12分)已知平行四边形![]() 的三个顶点的坐标为
的三个顶点的坐标为![]() ,
,![]() ,
,![]() .
.
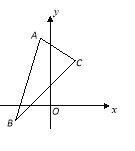
(Ⅰ)在![]() ABC中,求边AC中线所在直线方程;
ABC中,求边AC中线所在直线方程;
(Ⅱ)求平行四边形![]() 的顶点D的坐标及边BC的长度;
的顶点D的坐标及边BC的长度;
(Ⅲ)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线![]() 的参数方程是
的参数方程是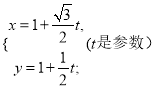
(I)写出直线![]() 的极坐标方程;
的极坐标方程;
(II)设![]() 与圆
与圆![]() 相交于两点A、B,求点P到A、B两点的距离之积
相交于两点A、B,求点P到A、B两点的距离之积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com