
对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称点
成立,则称点![]() 为函数的不动点。
为函数的不动点。
(1)已知函数![]() 有不动点(1,1)和(-3,-3)求
有不动点(1,1)和(-3,-3)求![]() 与
与![]() 的值;
的值;
(2)若对于任意实数![]() ,函数
,函数![]() 总有两个相异的不动点,求
总有两个相异的不动点,求![]() 的取值范围;
的取值范围;
(3)若定义在实数集R上的奇函数![]() 存在(有限的)
存在(有限的)![]() 个不动点,求证:
个不动点,求证:![]() 必为奇数。
必为奇数。
(1)![]() ,
,![]() (2)
(2)![]() (3)见解析
(3)见解析
(1)由不动点的定义:![]() ,∴
,∴![]() …….1’
…….1’
代入![]() 知
知![]() ,又由
,又由![]() 及
及![]() 知
知![]() 。……………………...2’
。……………………...2’
∴![]() ,
,![]() 。 …………………………....................1’
。 …………………………....................1’
(2)对任意实数![]() ,
,![]() 总有两个相异的不动点,即是对任意的实数
总有两个相异的不动点,即是对任意的实数![]() ,方程
,方程![]() 总有两个相异的实数根。...........1’
总有两个相异的实数根。...........1’
∴![]() 中
中![]() ,
,
即![]() 恒成立。………………………....................2’
恒成立。………………………....................2’
故![]() ,∴
,∴![]() 。………….........................2’
。………….........................2’
故当![]() 时,对任意的实数
时,对任意的实数![]() ,方程
,方程![]() 总有两个相异的不动点。 ………...................1’
总有两个相异的不动点。 ………...................1’
(3)![]() 是R上的奇函数,则
是R上的奇函数,则![]() ,∴(0,0)是函数
,∴(0,0)是函数![]() 的不动点。 ……..................1’
的不动点。 ……..................1’
若![]() 有异于(0,0)的不动点
有异于(0,0)的不动点![]() ,则
,则![]() 。
。
又![]() ,∴
,∴![]() 是函数
是函数![]() 的不动点。
的不动点。
∴![]() 的有限个不动点除原点外,都是成对出现的, ..........................4’
的有限个不动点除原点外,都是成对出现的, ..........................4’
所以有![]() 个(
个(![]() ),加上原点,共有
),加上原点,共有![]() 个。即
个。即![]() 必为奇数
必为奇数


科目:高中数学 来源: 题型:
对于函数![]() ,若存在
,若存在![]() 成立,则称
成立,则称![]() 的不动点。如果函数
的不动点。如果函数![]() 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且![]()
(1)求函数![]() 的解析式;
的解析式;
(2)已知各项不为零的数列![]() ,求数列通项
,求数列通项![]() ;
;
(3)如果数列![]() 满足
满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源:2011届河南省卫辉市第一中学高三一月月考数学理卷 题型:解答题
(本小题满分12分)
对于函数 ,若存在
,若存在 R,使
R,使 成立,则称
成立,则称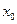 为
为 的不动点.如果函数
的不动点.如果函数 N*
N* 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且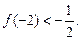
(1)求实数 ,
, 的值;
的值;
(2)已知各项不为零的数列
 ,并且
,并且 , 求数列
, 求数列 的通项公式;;
的通项公式;;
(3)求证: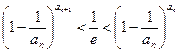 .
.
查看答案和解析>>
科目:高中数学 来源:2013届海南省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
对于函数 ,若存在实数
,若存在实数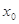 ,使
,使 成立,则称
成立,则称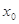 为
为 的不动点.
的不动点.
⑴当 时,求
时,求 的不动点;
的不动点;
⑵若对于任何实数 ,函数
,函数 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数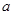 的取值范围;
的取值范围;
⑶在⑵的条件下,若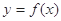 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数 的不动点,且直线
的不动点,且直线 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三12月月考理科数学卷 题型:解答题
(本小题满分12分)
对于函数 ,若存在
,若存在 R,使
R,使 成立,则称
成立,则称 为
为 的不动点.如果函数
的不动点.如果函数 N*
N* 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且
(1)求实数 ,
, 的值;
的值;
(2)已知各项不为零的数列
 ,并且
,并且 , 求数列
, 求数列 的通项公式;;
的通项公式;;
(3)求证: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com