
【题目】已知以![]() 为焦点的抛物线
为焦点的抛物线![]() 过点
过点![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 中点,且
中点,且![]() .
.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将![]() 代入抛物线方程,求得
代入抛物线方程,求得![]() 的值,根据向量的坐标运算,即可求得
的值,根据向量的坐标运算,即可求得![]() 的值;
的值;
(2)方法一:根据向量的坐标运算,求得![]() 的纵坐标,利用抛物线的“点差法”求得直线的斜率,代入抛物线方程,利用韦达定理及向量的坐标运算,即可求得直线
的纵坐标,利用抛物线的“点差法”求得直线的斜率,代入抛物线方程,利用韦达定理及向量的坐标运算,即可求得直线![]() 的方程;
的方程;
方法二:设直线![]() 的方程,代入抛物线方程,利用韦达定理,中点坐标公式,及向量的坐标运算,即可求得直线
的方程,代入抛物线方程,利用韦达定理,中点坐标公式,及向量的坐标运算,即可求得直线![]() 的方程.
的方程.
解:(1)将![]() 代入抛物线
代入抛物线![]() 方程,得
方程,得![]() ,
,
所以![]() 的方程为
的方程为![]() ,焦点
,焦点![]() ,
,
设![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,可得
,可得![]() .
.
(2)方法一:设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() .可得
.可得![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
所以直线![]() 的斜率存在且斜率
的斜率存在且斜率![]() ,
,
设直线![]() 的方程为
的方程为![]() ,联立
,联立![]() ,消去
,消去![]() ,
,
整理得![]() ,
,
△![]() ,可得
,可得![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
解得![]() ,
,![]() (舍
(舍![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
方法二:设直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立方程组![]() ,消去
,消去![]() ,
,
整理得![]() ,△
,△![]() ,
,
则![]() ,
,![]() ,
,
则![]() ,
,
则![]() ,
,![]() ,由
,由![]() .
.
得![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
由△![]() ,可得
,可得![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,
,
解得![]() 或
或![]() ,(舍去)
,(舍去)
所以直线![]() 的方程为
的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】今年消毒液和口罩成了抢手年货,老百姓几乎人人都需要,但对于![]() 这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于
这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于![]() 这种口罩了解的占
这种口罩了解的占![]() ,其中45岁以上(含45岁)的人数占
,其中45岁以上(含45岁)的人数占![]() .
.
(1)将答题卡上的列联表补充完整;
(2)判断是否有![]() 的把握认为对
的把握认为对![]() 这种口罩的了解与否与年龄有关.
这种口罩的了解与否与年龄有关.
参考公式: ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所有抽取的30岁以上的网民中利用分层抽样抽取5人,
![]() 求这5人中经常使用、偶尔或不用共享单车的人数;
求这5人中经常使用、偶尔或不用共享单车的人数;
![]() 从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 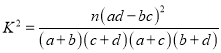 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536—1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为![]() ,第八个音的频率为
,第八个音的频率为![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥S—ABCD中,底面ABCD为长方形,SB⊥底面ABCD,其中BS=2,BA=2,BC=λ,λ的可能取值为:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤λ=3
;⑤λ=3

(1)求直线AS与平面ABCD所成角的正弦值;
(2)若线段CD上能找到点E,满足AE⊥SE,则λ可能的取值有几种情况?请说明理由;
(3)在(2)的条件下,当λ为所有可能情况的最大值时,线段CD上满足AE⊥SE的点有两个,分别记为E1,E2,求二面角E1-SB-E2的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com