
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
| 成绩 | 2a=6,
|
a=3,c=
|
|
|
△=144k2-12(1+3k2)>0, | |||||||||||||||||||||
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | k2>
|
A(x1,y1),B(x2,y2) | x1+x2=
|
y1+y2=k(x1+x2)-4=k•
|
E(
| ||||||||||||||
| 频数 | 1 | 11 | 23 | 13 | 2 |
| 成绩小于100分 | 成绩不小于100分 | 合计 | |||||||
| 甲班 |
|
26 | 50 | ||||||
| 乙班 | 12 | k=±1 | 50 | ||||||
| 合计 | 36 | 64 | 100 |
| x-y-2=0或x+y+2=0. | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | ||
a=
|
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2014届广东珠海市高二下学期期末考试文科数学试卷(B卷)(解析版) 题型:解答题
考察某种药物预防甲型H1N1流感的效果,进行动物试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(Ⅰ)根据所给样本数据完成下面2×2列联表;
(Ⅱ)请问能有多大把握认为药物有效?
|
|
不得流感 |
得流感 |
总计 |
|
服药 |
|
|
|
|
不服药 |
|
|
|
|
总计 |
|
|
|
(参考数据: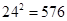 )
)
查看答案和解析>>
科目:高中数学 来源:2013届吉林省吉林市高二期中考试文科数学试卷(解析版) 题型:解答题
为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(Ⅰ)根据所给样本数据完成下面2×2列联表;
(Ⅱ)请问能有多大把握认为药物有效?
|
|
不得禽流感 |
得禽流感 |
总计 |
|
服药 |
|
|
|
|
不服药 |
|
|
|
|
总计 |
|
|
|
参考公式: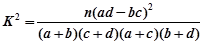
|
|
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0. 025 |
0.010 |
0.005 |
0.001 |
|
|
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com