
【题目】已知函数f(x)![]() ,
,
(1)讨论函数f(x)的单调性;
(2)证明:a=1时,f(x)+g(x)﹣(1![]() )lnx>e.
)lnx>e.
【答案】(1)详见解析;(2)证明见解析
【解析】
(1)对![]() 求导后,再对a分类讨论即可得出函数的单调性.
求导后,再对a分类讨论即可得出函数的单调性.
(2)a=1时,将所证不等式转化为ex﹣ex+1![]() ,令F(x)=ex﹣ex+1,G(x)
,令F(x)=ex﹣ex+1,G(x)![]() ,分别根据导数求出
,分别根据导数求出![]() 的最小值和
的最小值和![]() 的最大值即可证明不等式成立.
的最大值即可证明不等式成立.
(1)f(x)![]() alnx,(x∈(0,+∞)).
alnx,(x∈(0,+∞)).
![]()
![]() .
.
当a≤0时,![]() <0,函数f(x)在x∈(0,+∞)上单调递减.
<0,函数f(x)在x∈(0,+∞)上单调递减.
a>0时,由![]()
![]() ,得
,得![]() ,由
,由![]()
![]() ,得
,得![]()
所以函数![]() 在(0,
在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
(2)证明:a=1时,要证f(x)+g(x)﹣(1![]() )lnx>e.
)lnx>e.
即要证:![]() lnx﹣e>0ex﹣ex+1
lnx﹣e>0ex﹣ex+1![]() .x∈(0,+∞).
.x∈(0,+∞).
令F(x)=ex﹣ex+1,F′(x)=ex﹣e,
当x∈(0,1)时,F′(x)<0,此时函数F(x)单调递减;
当x∈(1,+∞)时,F′(x)>0,此时函数F(x)单调递增.
可得x=1时,函数F(x)取得最小值,F(1)=1.
令G(x)![]() ,G′(x)
,G′(x)![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 为增函数,
为增函数,
当![]() 时。
时。![]() ,此时
,此时![]() 为减函数
为减函数
所以x=e时,函数G(x)取得最大值,G(e)=1.
x=1与x=e不同时取得,因此F(x)>G(x),即ex﹣ex+1![]() .x∈(0,+∞).
.x∈(0,+∞).
故原不等式成立.


科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,![]() 为
为![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ).将
).将![]() 沿
沿![]() 折起,记折起后点
折起,记折起后点![]() 为
为![]() ,连接
,连接![]() 为
为![]() 上的一点,且
上的一点,且![]() ,连接
,连接![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,当
,当![]() 最大时,求
最大时,求![]() ,并计算
,并计算![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)为奇函数,且当x≥0时,f(x)=ex﹣cosx,则不等式f(2x﹣1)+f(x﹣2)>0的解集为( )
A.(﹣∞,1)B.(﹣∞,![]() )C.(
)C.(![]() ,+∞)D.(1,+∞)
,+∞)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场推出消费抽现金活动,顾客消费满1000元可以参与一次抽奖,该活动设置了一等奖、二等奖、三等奖以及参与奖,奖金分别为:一等奖200元、二等奖100元、三等奖50元、参与奖20元,具体获奖人数比例分配如图,则下列说法中错误的是( )

A.获得参与奖的人数最多
B.各个奖项中一等奖的总金额最高
C.二等奖获奖人数是一等奖获奖人数的两倍
D.奖金平均数为![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区城乡居民储蓄存款年底余额(单位:亿元)如图所示,下列判断一定不正确的是( )
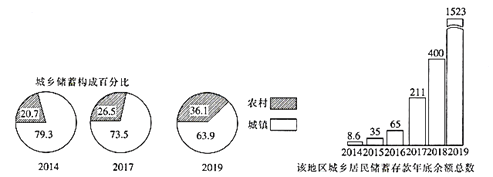
A.城乡居民储蓄存款年底余额逐年增长
B.农村居民的存款年底余额所占比重逐年上升
C.到2019年农村居民存款年底总余额已超过了城镇居民存款年底总余额
D.城镇居民存款年底余额所占的比重逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】角谷猜想,也叫![]() 猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取
猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取![]() ,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若
,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若![]() ,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com