
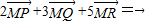 ,则三点P,Q,R共线;
,则三点P,Q,R共线; ,则三点P,Q,R共线;
,则三点P,Q,R共线;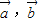 不共线,则关于x方程
不共线,则关于x方程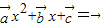 至多有一个实根;
至多有一个实根;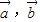 不共线,则关于x方程
不共线,则关于x方程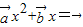 有唯一实根.
有唯一实根.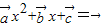 有一个实根,否则关于x方程
有一个实根,否则关于x方程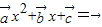 无实根,进而判断③的真假,若向量
无实根,进而判断③的真假,若向量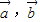 不共线,则关于x方程
不共线,则关于x方程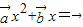 有唯一实根0,进而判断④的真假.
有唯一实根0,进而判断④的真假.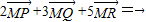 ,
,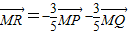 ,由于-
,由于- -
- =-1≠1,故P,Q,R三点不共线,故①错误;
=-1≠1,故P,Q,R三点不共线,故①错误;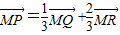 ,由于
,由于 +
+ =1,可得三点P,Q,R共线,故②正确;
=1,可得三点P,Q,R共线,故②正确;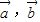 不共线,则存在唯一的实数对λ,μ使
不共线,则存在唯一的实数对λ,μ使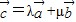 ,
,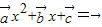 有一个实根,
有一个实根,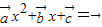 无实根,
无实根,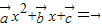 至多有一个实根,即③正确;
至多有一个实根,即③正确;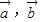 不共线,则关于x方程
不共线,则关于x方程 有唯一实根0,故④正确;
有唯一实根0,故④正确;

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
| AC |
| AB |
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
| OP |
| OA |
| AB |
| AC |
| OA |
| OB |
| OC |
| 0 |
| S△AOC |
| S△ABC |
| 1 |
| 3 |
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市黄浦区高三上学期期终基础学业测评理科数学试卷 题型:选择题
现给出如下命题:
(1)若直线 上有两个点到平面
上有两个点到平面 的距离相等,则直线
的距离相等,则直线 ;
;
(2)“平面 上有四个不共线的点到平面
上有四个不共线的点到平面 的距离相等”的充要条件是“平面
的距离相等”的充要条件是“平面 ”;
”;
(3)若一个球的表面积是 ,则它的体积
,则它的体积 ;
;
(4)若从总体中随机抽取的样本为 ,则该总体均值的点估计值是
,则该总体均值的点估计值是 .则其中正确命题的序号是
( )
.则其中正确命题的序号是
( )
A.(1)、(2)、(3). B.(1)、(2)、(4). C.(3)、(4). D.(2)、(3).
查看答案和解析>>
科目:高中数学 来源: 题型:
现给出如下命题:
(1)若直线![]() 与平面
与平面![]() 内无穷多条直线都垂直,则直线
内无穷多条直线都垂直,则直线![]() ;
;
(2)已知![]() ,则
,则![]() ;
;
(3)某种乐器发出的声波可用函数![]() 来描述,则该声波的频率是200赫兹;
来描述,则该声波的频率是200赫兹;
(4)样本数据![]() 的标准差是1.
的标准差是1.
则其中正确命题的序号是 [答]( )
A.(1)、(4). B.(1)、(3). C.(2)、(3)、(4). D.(3)、(4).
查看答案和解析>>
科目:高中数学 来源: 题型:
现给出如下命题:
(1)若直线与平面内无穷多条直线都垂直,则直线;
(2)空间三点确定一个平面;
(3) 先后抛两枚硬币,用事件A表示“第一次抛出现正面向上”,用事件B表示“第二次抛出现反面向上”,则事件A和B相互独立且=;
(4)样本数据的标准差是1.
则其中正确命题的序号是 [答]( )
A.(1)、(4). B.(1)、(3). C.(2)、(3)、(4). D.(3)、(4).
查看答案和解析>>
科目:高中数学 来源: 题型:
现给出如下命题:
(1)若直线与平面内无穷多条直线都垂直,则直线;
(2)空间三点确定一个平面;
(3) 先后抛两枚硬币,用事件A表示“第一次抛出现正面向上”,用事件B表示“第二次抛出现反面向上”,则事件A和B相互独立且=;
(4)样本数据的标准差是1.
则其中正确命题的序号是 [答]( )
A.(1)、(4). B.(1)、(3). C.(2)、(3)、(4). D.(3)、(4).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com