
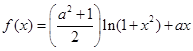
 .
.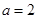 时,求
时,求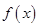 的极值;
的极值;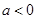 时,讨论
时,讨论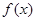 的单调性;
的单调性;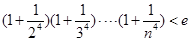 (
(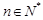 ,
,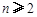 ,其中无理数
,其中无理数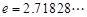 )
)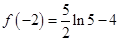 ,极小值
,极小值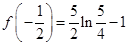 .(2)当
.(2)当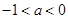 时,
时,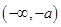 上单调递减,
上单调递减,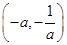 单调递增,
单调递增, 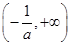 单调递减;当
单调递减;当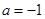 时,
时,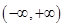 单调递减;当
单调递减;当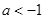 时,
时,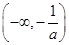 上单调递减,
上单调递减,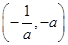 单调递增,
单调递增,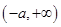 单调递减;(3)构造函数,利用函数的单调性处理
单调递减;(3)构造函数,利用函数的单调性处理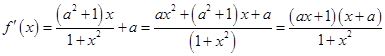 1分
1分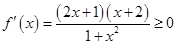 ,知
,知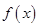 在区间
在区间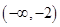 上单调递增,
上单调递增,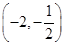 上单调递减,在单调递增.故有极大值
上单调递减,在单调递增.故有极大值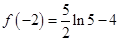 ,极小值
,极小值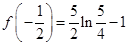 .………4分
.………4分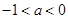 时,
时,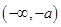 上单调递减,
上单调递减,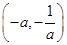 单调递增,
单调递增,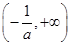 单调递减,当
单调递减,当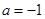 时,
时,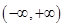 单调递减
单调递减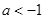 时,
时,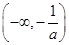 上单调递减,
上单调递减,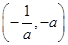 单调递增,
单调递增,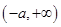 单调递减 7分
单调递减 7分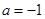 时,
时,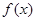 在
在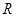 上单调递减.
上单调递减.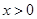 时
时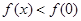
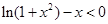 ,即
,即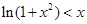
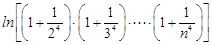
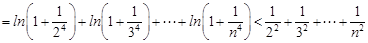
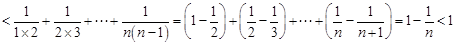
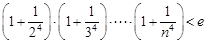 . 10分
. 10分

科目:高中数学 来源:不详 题型:解答题
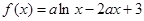 (
(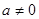 ).
).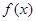 的单调区间;
的单调区间;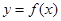 的图像在
的图像在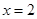 处的切线的斜率为
处的切线的斜率为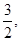 若函数
若函数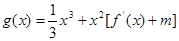 ,在区间(1,3)上不是单调函数,求
,在区间(1,3)上不是单调函数,求 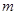 的取值范围。
的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com