
【题目】如图,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC=2.
(1)求证:平面AEF⊥平面PBC;
(2)求三棱锥P﹣AEF的体积.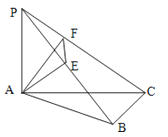
【答案】
解:(1)∵PA⊥平面ABC,BC平面ABC
∴PA⊥BC
又AB⊥BC
∴BC⊥平面PAB,而AE平面PAB
∴BC⊥AE
又AE⊥PB
∴AE⊥平面PBC
而AE平面AEF
∴平面平面AEF⊥平面PBC
(2)由(1)AE⊥平面PBC
又∵AF⊥PC
∴EF⊥PC(三垂线定理逆定理)
∴△PEF∽△PCB
∴![]()
∴S△PEF=![]() S△PBC=
S△PBC=![]()
∴VP﹣AEF=VA﹣PEF=![]() ×
×![]() ×
×![]() =
=![]()
【解析】(1)先根据条件得到PA⊥BC进而得BC⊥平面PAB,把问题转化为证AE⊥平面PBC即可;
(2)先根据第一问的结论以及三垂线定理逆定理可得△PEF∽△PCB,求出S△PEF , 再利用体积相等即可求出结论.
【考点精析】关于本题考查的平面与平面垂直的判定,需要了解一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.


科目:高中数学 来源: 题型:
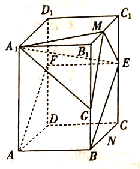
【题目】如图,四边形![]() 是正四棱柱
是正四棱柱![]() 的一个截面,此截面与棱
的一个截面,此截面与棱![]() 交于点
交于点![]() ,
, ![]() ,其中
,其中![]() 分别为棱
分别为棱![]() 上一点.
上一点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,若四面体
上一点,若四面体![]() 与四棱锥
与四棱锥![]() 的体积相等,求
的体积相等,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,且f(x)不为常值函数,有以下命题:
①函数g(x)=f(x)+f(﹣x)一定是偶函数;
②若对任意x∈R都有f(x)+f(2﹣x)=0,则f(x)是以2为周期的周期函数;
③若f(x)是奇函数,且对于任意x∈R,都有f(x)+f(2+x)=0,则f(x)的图象的对称轴方程为x=2n+1(n∈Z);
④对于任意的x1 , x2∈R,且x1≠x2 , 若![]() >0恒成立,则f(x)为R上的增函数,
>0恒成立,则f(x)为R上的增函数,
其中所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组中,f(x)与g(x)表示同一函数的是( )
A.f(x)=x, ![]()
B.f(x)=x, ![]()
C.f(x)=x2 , ![]()
D.f(x)=|x|,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且f(x)在(﹣∞,0]上单调递减,则不等式f(lgx)>f(﹣2)的解集是( )
A.( ![]() ,100)
,100)
B.(100,+∞)
C.( ![]() ,+∞)
,+∞)
D.(0, ![]() )∪(100,+∞)
)∪(100,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中![]() 表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.
表示每件药材的重量,则图中①,②两处依次应该填的整数分别是____________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合A={(x,y)|y=a},集合B={(x,y)|y=bx+1,b>0,b≠1},若集合A∩B≠,则实数a的取值范围是( )
A.(﹣∞,1)
B.(﹣∞,1]
C.[1,+∞)
D.(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com