练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数且

    （1）讨论的单调区间；

    （2）若直线的图象恒在函数图象的上方，求的取值范围.

    【答案】（1）在区间上是增函数；在区间上是减函数（2）

    【解析】试题分析：

    (1)由题意可得：且．分类讨论：当时，和当时，函数的单调区间即可；

    (2)很明显 时不合题意；当时，令，将问题转化为恒成立时的取值范围．由函数的性质可知： ．

    试题解析：

    （1）的定义域为，且．

    ①当时，∵，∴，∴，函数在是增函数；

    ②当时， ，在区间上， ；在区间上， ．

    所以在区间上是增函数；在区间上是减函数．

    （2）当时，取，则，

    不合题意．

    当时，令，则．

    问题转化为恒成立时的取值范围．

    由于，所以在区间上， ；在区间上， ．所以的最小值为，所以只需，即，所以，所以．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}，{bn}满足a1=1，an+1=2an+1，b1=4，bn﹣bn﹣1=an+1（n≥2）．
    （1）求证：数列{an+1}是等比数列；
    （2）求数列{an}，{bn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知： 、 、 是同一平面内的三个向量，其中 =（1，2）
    （1）若| |=2 ，且 ∥ ，求 的坐标；
    （2）若| |= ，且 +2 与2 ﹣ 垂直，求v与 的夹角θ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

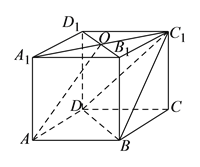
    【题目】在四棱柱中，底面，底面为菱形，为与交点，已知，．

    （I）求证：平面．

    （II）在线段上是否存在一点，使得平面，如果存在，求的值，如果不存在，请说明理由．

    （III）设点在内（含边界），且，求所有满足条件的点构成的图形，并求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）的最小正周期和单调递增区间；

    （Ⅱ）已知a，b，c是△ABC三边长，且f（C）=2，△ABC的面积S=，c=7．求角C及a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的方程2x2﹣（ +1）x+m=0的两根为sinθ和cosθ，θ∈（0，π）．求：
    （1）m的值；
    （2）+ 的值；
    （3）方程的两根及此时θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数y=sin2x（x∈R）图象上所有的点向左平移 个单位长度，所得图象的函数解析式为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列为公差不为的等差数列， 为前项和， 和的等差中项为，且．令数列的前项和为．

    （1）求及；

    （2）是否存在正整数成等比数列？若存在，求出所有的的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家电公司销售部门共有200位销售员，每位部门对每位销售员都有1400万元的年度销售任务，已知这200位销售员去年完成销售额都在区间（单位：百万元）内，现将其分成5组，第1组，第2组，第3组，第4组，第5组对应的区间分别为， ， ， ， ，绘制出频率分布直方图.

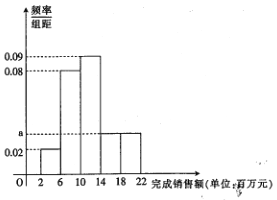
    （1）求的值，并计算完成年度任务的人数；

    （2）用分层抽样从这200位销售员中抽取容量为25的样本，求这5组分别应抽取的人数；

    （3）现从（2）中完成年度任务的销售员中随机选取2位，奖励海南三亚三日游，求获得此奖励的2位销售员在同一组的概率.

    查看答案和解析>>

    同步练习册答案