
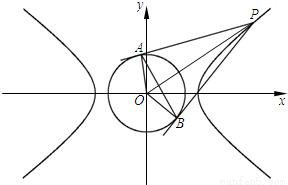
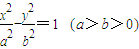 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.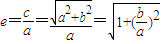
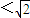 .由∠APB=90°及圆的性质,知四边形PAOB是正方形,所以
.由∠APB=90°及圆的性质,知四边形PAOB是正方形,所以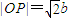 .由此能求出双曲线离心率e的取值范围.
.由此能求出双曲线离心率e的取值范围.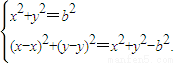 ,得直线AB的方程.
,得直线AB的方程.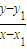 ,
,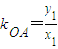 (其中x1≠x,x1≠0).因为PA⊥OA,所以kPAkOA=-1,即
(其中x1≠x,x1≠0).因为PA⊥OA,所以kPAkOA=-1,即 .因为OA=OB,PA=PB,根据平面几何知识可知,AB⊥OP.因为
.因为OA=OB,PA=PB,根据平面几何知识可知,AB⊥OP.因为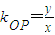 ,所以
,所以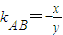 .由此能求出直线AB的方程.
.由此能求出直线AB的方程.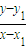 ,
,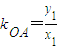 .因为PA⊥OA,所以
.因为PA⊥OA,所以 .由此能求出直线AB的方程.
.由此能求出直线AB的方程. .由
.由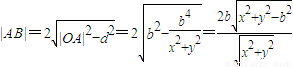 ,知△OAB的面积
,知△OAB的面积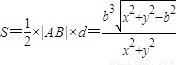 .以下给出求三角形OAB的面积S的三种方法:
.以下给出求三角形OAB的面积S的三种方法: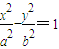 上,所以
上,所以 .设
.设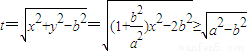 ,所以
,所以 .再由导数能够求出
.再由导数能够求出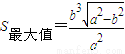 .
.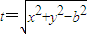 ,则
,则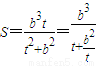 .因为点P(x,y)在双曲线
.因为点P(x,y)在双曲线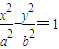 上,所以
上,所以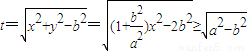 .令
.令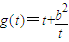 ,再由导数能够求出
,再由导数能够求出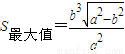 .
.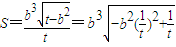 .因为点P(x,y)在双曲线
.因为点P(x,y)在双曲线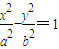 上,所以
上,所以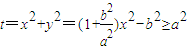 .令
.令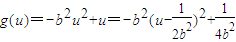 ,所以g(u)在
,所以g(u)在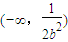 上单调递增,在
上单调递增,在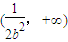 上单调递减.由此能够求出
上单调递减.由此能够求出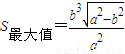 .
.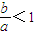 ,所以
,所以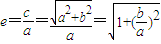
 .(1分)
.(1分) .
.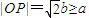 ,所以
,所以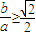 ,所以
,所以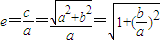
 .(3分)
.(3分)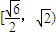 .(4分)
.(4分)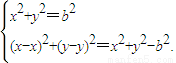 (7分)
(7分)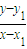 ,
,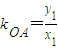 (其中x1≠x,x1≠0).
(其中x1≠x,x1≠0).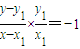 .(5分)
.(5分)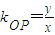 ,所以
,所以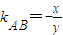 .(7分)
.(7分)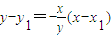 .
.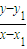 ,
,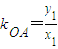 (其中x1≠x,x1≠0).
(其中x1≠x,x1≠0).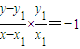 .
. 整理得xx1+yy1=x12+y12.
整理得xx1+yy1=x12+y12.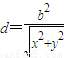 .
.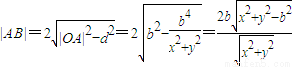 ,
,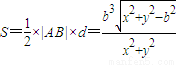 .(10分)
.(10分)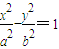 上,
上,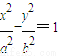 ,即
,即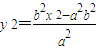 (x2≥a2).
(x2≥a2).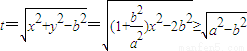 ,
,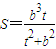 .(11分)
.(11分)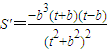 ,
,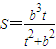 在(0,b)上单调递增,在(b,+∞)上单调递减.(12分)
在(0,b)上单调递增,在(b,+∞)上单调递减.(12分)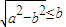 ,即
,即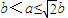 时,
时, ,(13分)
,(13分)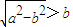 ,即
,即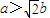 时,
时,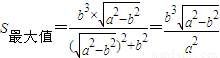 .
.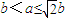 时,
时, ;当
;当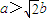 时,
时,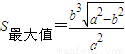 .(14分)
.(14分)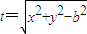 ,则
,则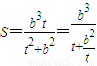 .(11分)
.(11分)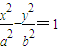 上,即
上,即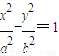 ,即
,即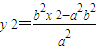 (x2≥a2).
(x2≥a2).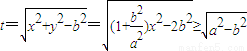 .
.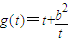 ,则
,则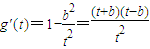 .
.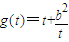 在(0,b)上单调递减,在(b,+∞)上单调递增.(12分)
在(0,b)上单调递减,在(b,+∞)上单调递增.(12分)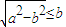 ,即
,即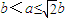 时,
时,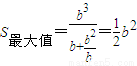 ,(13分)
,(13分)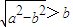 ,即
,即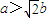 时,
时,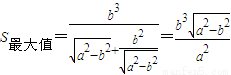 .
.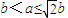 时,
时, ;当
;当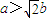 时,
时, .(14分)
.(14分)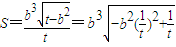 .(11分)
.(11分)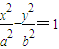 上,即
上,即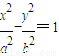 ,即
,即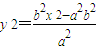 (x2≥a2).
(x2≥a2).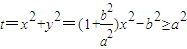 .
.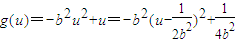 ,
,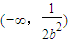 上单调递增,在
上单调递增,在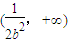 上单调递减.(12分)
上单调递减.(12分)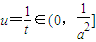 ,
,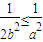 ,即
,即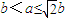 时,
时,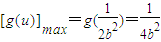 ,此时
,此时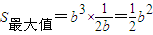 .
.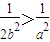 ,即
,即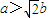 时,
时,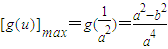 ,此时
,此时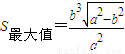 .
.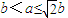 时,
时, ;当
;当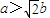 时,
时,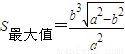 .(14分)
.(14分)

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:浙江省兰溪一中2010-2011学年高二下学期期中考试数学理科试题 题型:044
已知双曲线C: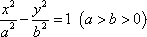 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A、B.
(1)若双曲线C上存在点P,使得∠APB=90°,求双曲线离心率e的取值范围;
(2)求直线AB的方程;
(3)求三角形OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源:广东省模拟题 题型:解答题
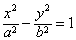 (a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。
(a>b>0)和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x0,y0)引圆O的两条切线,切点分别为A,B。查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省金华市兰溪一中高二(下)期中数学试卷(理科)(解析版) 题型:解答题
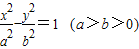 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.查看答案和解析>>
科目:高中数学 来源:2011年广东省广州市高考数学二模试卷(文科)(解析版) 题型:解答题
 和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.
和圆O:x2+y2=b2(其中原点O为圆心),过双曲线C上一点P(x,y)引圆O的两条切线,切点分别为A、B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com