练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图F1(－c，0)，F2(c，0)为双曲线E的两焦点，以F1F2为直径的圆O与双曲线E交于M、N、M1、N1，B是圆O与y轴的交点，连接MM1与OB交于H，且H是OB的中点，

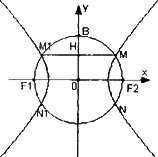
    (1)当c＝1时，求双曲线E的方程；

    (2)试证：对任意的正实数c，双曲线E的离心率为常数．

    答案：
    解析：

    　　解：(1)由c＝1有B(0，1)，

    　　设E：

    　　　　　7分

    　　(2)

    　　设E：

    　　为常数．　　7分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

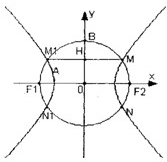    如图F1（-c，0），F2（c，0）为双曲线E的两焦点，以F1F2为直径的圆O与双曲线E交于M、N、M1、N1，B是圆O与y轴的交点，连接MM1与OB交于H，且H是OB的中点．
    （1）当c=1时，求双曲线E的方程；
    （2）试证：对任意的正实数c，双曲线E的离心率为常数；
    （3）连接F1M与双曲线E交于点A，是否存在常数λ，使
    F1A
    =λ
    AM
    恒成立，若存在试求出λ的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，椭圆C：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的顶点为A1、A2、B1、B2，焦点为F1，
    F2，|A1B1|=
    		7
    ，
    S?A1B1A2B 2=2S?B1F1B2F 2
    （1）求椭圆C的方程；
    （2）设l是过原点的直线，直线n与l垂直相交于P点，且n与椭圆相交于A，B两点，|OP|=1，求
    AP
    •
    PB
    的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：冷水江市一中2007届高三第十次模拟考试理科数学试卷 题型：044

    如图F1(－c，0)F2(c，0)为双曲线E的两焦点，以F1F2为直径的圆O与双曲线E交于M、N、M1、N1，B是圆O与y轴的交点，连接MM1与OB交于H，且H是OB的中点，

    (1)当c＝1时，求双曲线E的方程；(4分)

    (2)试证：对任意的正实数c，双曲线E的离心率为常数；(4分)

    (3)连接F1M与双曲线E交于点A，是否存在常数恒成立，若存在试求出λ的值；若不存在，请说明理由．(5分)

    查看答案和解析>>

    科目：高中数学 来源：江苏省常州高级中学2007～2008学年第三次阶段教学质量调研高三数学(文科) 题型：044

    如图F1(－c，0)，F2(c，0)为双曲线E的两焦点，以F1F2为直径的圆O与双曲线E交于M、N、M1、N1，B是圆O与y轴的交点，连接MM1与OB交于H，且H是OB的中点，

    (1)当c＝1时，求双曲线E的方程；

    (2)试证：对任意的正实数c，双曲线E的离心率为常数；

    (3)连接F1M与双曲线E交于点A，是否存在常数恒成立，若存在试求出λ的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案