
 ,动点P满足条件:
,动点P满足条件: ,点P的轨迹是曲线E,直线l:y=kx-1与曲线E交于A、B两点.如果
,点P的轨迹是曲线E,直线l:y=kx-1与曲线E交于A、B两点.如果 .
. ,求m的值.
,求m的值.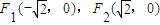 为焦点,
为焦点,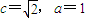 的双曲线的左支,从而写出曲线E的方程,再设A(x1,y1),B(x2,y2),把y=kx-1代入双曲线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得k值,从而解决问题.
的双曲线的左支,从而写出曲线E的方程,再设A(x1,y1),B(x2,y2),把y=kx-1代入双曲线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得k值,从而解决问题.
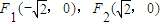 为焦点,
为焦点,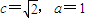 的双曲线的左支,
的双曲线的左支,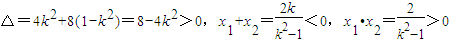
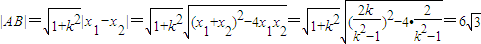
 (∵
(∵ )
)
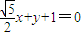 .
.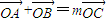 ,得(x1+x2,y1+y2)=(mx,my)
,得(x1+x2,y1+y2)=(mx,my)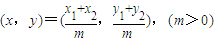


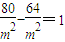 .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源:2007年贵州省普通高等学校招生适应性考试数学(理) 题型:044
已知定点![]() ,动点P满足条件:
,动点P满足条件:![]() ,点P的轨迹是曲线E,直线l:y=kx-1与曲线E交于A、B两点.如果
,点P的轨迹是曲线E,直线l:y=kx-1与曲线E交于A、B两点.如果![]() .
.
(Ⅰ)求直线l的方程;
(Ⅱ)若曲线E上存在点C,使![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:高中数学 来源:2007年贵州省普通高等学校招生适应性考试数学(文) 题型:044
已知定点![]() ,动点P满足条件:
,动点P满足条件:![]() ,点P的轨迹是曲线E,直线l:y=kx-1与曲线E交于A、B两点.如果
,点P的轨迹是曲线E,直线l:y=kx-1与曲线E交于A、B两点.如果![]() .
.
(Ⅰ)求直线l的方程;
(Ⅱ)若曲线E上存在点C,使![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com