
【题目】已知二次函数![]() 满足:①
满足:①![]() ,有
,有![]() ;②
;②![]() ;③
;③![]() 的图像与x轴两交点间距离为4.
的图像与x轴两交点间距离为4.
(1)求![]() 的解析式;
的解析式;
(2)记![]() ,
,![]() .
.
①若![]() 为单调函数,求k的取值范围;
为单调函数,求k的取值范围;
②记![]() 的最小值为
的最小值为![]() ,讨论
,讨论![]() 的零点个数.
的零点个数.
【答案】(1)![]()
(2)①![]() 或
或![]() ;②
;②![]() 时无零点;
时无零点;![]() 时,有4个零点,
时,有4个零点,![]() 时,有3个零点,
时,有3个零点,![]() 或
或![]() 时,有2个零点
时,有2个零点
【解析】
(1)设出二次函数解析式,根据已知条件得到二次函数对称轴、与![]() 轴交点、根与系数关系,由此列方程组,解方程组求得二次函数解析式
轴交点、根与系数关系,由此列方程组,解方程组求得二次函数解析式
(2)①求得![]() 解析式,根据其对称轴与区间
解析式,根据其对称轴与区间![]() 的位置关系,求得
的位置关系,求得![]() 的取值范围.
的取值范围.
②将![]() 分成
分成![]() ,
,![]() ,
,![]() 三种情况,结合
三种情况,结合![]() 的单调性,求得
的单调性,求得![]() 的表达式,利用换元法:令
的表达式,利用换元法:令![]() ,即
,即![]() ,结合
,结合![]() 的图像对
的图像对![]() 进行分类讨论,由此求得
进行分类讨论,由此求得![]() 的零点个数.
的零点个数.
(1)设![]() ,由题意知对称轴
,由题意知对称轴![]() ;①
;①
![]() ;②
;②
设![]() 的两个根为
的两个根为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
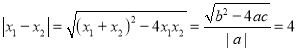 ;③
;③
由①②③解得![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
(2)①![]() ,其对称轴
,其对称轴![]() .
.
由题意知:![]() 或
或![]() ,
,
∴![]() 或
或![]() .
.
②
1)当![]() 时,对称轴
时,对称轴![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
2)当![]() 时,对称轴
时,对称轴![]() ,
,![]() ,
,
3)当![]() 时,对称轴
时,对称轴![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
![]() ,
,
∴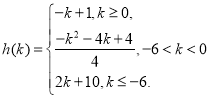 ,
,
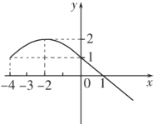
令![]() ,即
,即![]() ,画出
,画出![]() 简图,
简图,
i)当![]() 时,
时,![]() ,
,![]() 或0,
或0,
∴![]() 时,解得
时,解得![]() ,
,
![]() 时,解得
时,解得![]() ,有3个零点.
,有3个零点.
ii)当![]() 时,
时,![]() 有唯一解
有唯一解![]() ,
,![]() ,
,
![]() 有2个零点.
有2个零点.
iii)当![]() 时,
时,![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,
,
且![]() ,
,![]() ,
,
∴![]() 时,解得
时,解得![]() ,
,
![]() 时,解得
时,解得![]() ,有4个不同的零点.
,有4个不同的零点.
iv)当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() 有2个零点.
有2个零点.
v)当![]() 时,
时,![]() 无解.
无解.
综上所得:
![]() 时无零点;
时无零点;
![]() 时,有4个零点;
时,有4个零点;
![]() 时,有3个零点;
时,有3个零点;
![]() 或
或![]() 时,有2个零点.
时,有2个零点.


科目:高中数学 来源: 题型:
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() :
:![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 的两条直线
的两条直线![]() 、
、![]() 分别交抛物线
分别交抛物线![]() 于点
于点![]() 、
、![]() 和
和![]() 、
、![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() 、
、![]() .如果直线
.如果直线![]() 与
与![]() 的倾斜角互余,求证:直线
的倾斜角互余,求证:直线![]() 经过一定点.
经过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,03,![]() ,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1) 若把曲线![]() 上的点的横坐标不变,纵坐标伸长到原来的2倍,得到曲线
上的点的横坐标不变,纵坐标伸长到原来的2倍,得到曲线![]() ,求
,求![]() 的极坐标方程;
的极坐标方程;
(2) 直线![]() 的极坐标方程是
的极坐标方程是![]() ,与曲线
,与曲线![]() 交于
交于![]() 两点,求三角形
两点,求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大衍数列,来源于《乾坤谱》中对易传“大衍之数五十“的推论.主要用于解释中国传统文化中的太极衍生原理数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和是中华传统文化中隐藏着的世界数学史上第一道数列题其规律是:偶数项是序号平方再除以2,奇数项是序号平方减1再除以2,其前10项依次是0,2,4,8,12,18,24,32,40,50,…,如图所示的程序框图是为了得到大衍数列的前100项而设计的,那么在两个判断框中,可以先后填入( )

A. ![]() 是偶数?,
是偶数?,![]() ? B.
? B. ![]() 是奇数?,
是奇数?,![]() ?
?
C. ![]() 是偶数?,
是偶数?, ![]() ? D.
? D. ![]() 是奇数?,
是奇数?,![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某船在海面![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向,与
方向,与![]() 相距
相距![]() 海里,测得灯塔
海里,测得灯塔![]() 在北偏西
在北偏西![]() 方向,与
方向,与![]() 相距
相距![]() 海里,船由
海里,船由![]() 向正北方向航行到
向正北方向航行到![]() 处,测得灯塔
处,测得灯塔![]() 在南偏西
在南偏西![]() 方向,这时灯塔
方向,这时灯塔![]() 与
与![]() 相距多少海里?
相距多少海里?![]() 在
在![]() 的什么方向?
的什么方向?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=3-x,g(x)=log3(x+8).
(1)求f(1),g(1),f[g(1)],g[f(1)]的值;
(2)求f[g(x)],g[f(x)]的表达式并说明定义域;
(3)说明f[g(x)],g[f(x)]的单调性(不需要证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com