
 如图,在△AOB中,∠OAB=
如图,在△AOB中,∠OAB=| π |
| 6 |
| 1 |
| 2 |
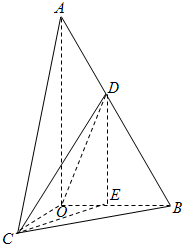 解:(I)证明:由题意,CO⊥AO,BO⊥AO,∴∠BOC是二面角B-AO-C是直二面角,
解:(I)证明:由题意,CO⊥AO,BO⊥AO,∴∠BOC是二面角B-AO-C是直二面角,| 1 |
| 2 |
| CO2+OE2 |
2
| ||
| 3 |
| 2 |
| 3 |
4
| ||
| 3 |
| CE |
| DE |
| ||
| 6 |
| ||
| 6 |
| OC |
| OD |
| 2 |
| OD |
| OA•OB |
| AB |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |


科目:高中数学 来源: 题型:
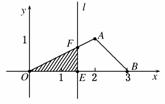
如图,在△AOB中,点A(2,1),B(3,0),点E在射线OB上自O开始移动.设OE=x,过E作OB的垂线l,记△AOB在直线l左边部分的面积为S,试写出S与x的函数关系式,并画出大致的图象.
查看答案和解析>>
科目:高中数学 来源:《2.1-2.3 平面向量的概念、线性、基本定理及坐标表示》2013年同步练习(解析版) 题型:解答题
 如图,在△AOB中,点P在直线AB上,且满足
如图,在△AOB中,点P在直线AB上,且满足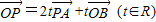 ,求
,求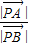 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com