
(10分)不等式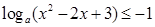 ,当
,当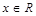 时恒成立.求
时恒成立.求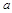 的取值范围.
的取值范围.
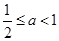 。
。
【解析】
试题分析:由已知得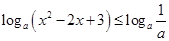 ....................1分
....................1分
(1)当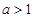 时
时
则 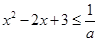 ................2分
................2分
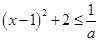 ①
......................3分
①
......................3分
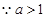
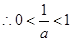 .....................4分
.....................4分
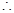 ①式无实数解....................................5分
①式无实数解....................................5分
(2)当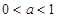 时
时
则 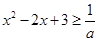
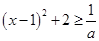 ......................6分
......................6分
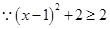 ................7分
................7分
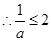
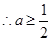 ......................8分
......................8分
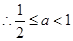 ..............9分
..............9分
综合以上两种情况可知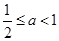 。 ....................10分
。 ....................10分
考点:本题主要考查对数函数的性质及其应用,二次函数图象和性质。
点评:典型题,复合对数函数问题,应特别注意其自身定义域。本题首先化成关于对数函数的二次函数,利用二次函数图象和性质得到所求范围。


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源:2013-2014学年江西九江市等七校高三联考理科数学试卷(解析版) 题型:解答题
已知向量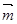
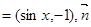
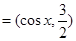 ,
,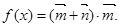
(Ⅰ)当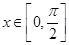 时,求函数
时,求函数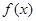 的值域;
的值域;
(Ⅱ)不等式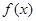 ≤
≤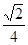
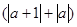 ,当
,当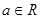 时恒成立,求
时恒成立,求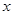 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com