
【题目】已知二次函数![]() ,设
,设![]() 是函数
是函数![]() 在
在![]() 上的最大值.
上的最大值.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的解析式;
的解析式;
(2)若对任意的![]() ,恒有
,恒有![]() ,求满足条件的所有实数对
,求满足条件的所有实数对![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:本题表面上是新定义问题,实质上新定义仅仅是最大值的另一种说法,(1)问题就是求![]() 在区间
在区间![]() 上的最大值,由于绝对值符号里面的式子
上的最大值,由于绝对值符号里面的式子![]() 是二次的,对称轴是
是二次的,对称轴是![]() ,因此其在区间
,因此其在区间![]() 上递减,从而只要考虑
上递减,从而只要考虑![]() 和
和![]() 的大小可得结论;(2)首先要求
的大小可得结论;(2)首先要求![]() ,从(1)的研究知,须按
,从(1)的研究知,须按![]() 对称轴与区间的关系分类,当
对称轴与区间的关系分类,当![]() 或
或![]() 时,
时,![]() 在区间
在区间![]() 上单调,因此有
上单调,因此有![]() ,
,![]() ,下面对此式进行放缩,有
,下面对此式进行放缩,有![]()
![]()
![]()
![]() ,研究这里三个不等号取等号的条件可得
,研究这里三个不等号取等号的条件可得![]() ,当
,当![]() 时,还需分类讨论到底有
时,还需分类讨论到底有![]() 还是有
还是有![]() ,(按
,(按![]() 的大小分类,也即1,2哪个离对称轴远),同上进行放缩以求得取最小值时的
的大小分类,也即1,2哪个离对称轴远),同上进行放缩以求得取最小值时的![]() ,比较
,比较![]() 的最小值可得
的最小值可得![]() .
.
试题解析:(1)当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,故
上单调递减,故![]() 在
在![]() 上的值域为
上的值域为![]() .
.
从而![]() ;
;
(2)函数![]() 的对称轴为
的对称轴为![]() ,下面讨论
,下面讨论![]() 的大小关系来确定
的大小关系来确定![]() 的单调性.
的单调性.
①当![]() 或
或![]() 时,
时,![]() 在
在![]() 上单调,又
上单调,又![]() ,
,![]() ,
,
![]()
![]()
不等号1,2,3取到等号的条件分别为 或
或 ,
,
从而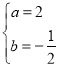 或
或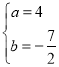
②当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,又
上单调递减,又![]() ,
,
![]() ,
,![]()
ⅰ)当![]() 时,
时,![]()
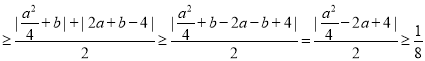
不等号1,2,3取到等号的条件分别为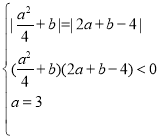 ,故
,故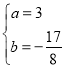 .
.
ⅱ)当![]() 时,
时,![]()
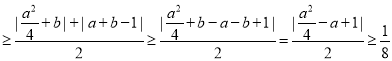
不等号1,2,3取到等号的条件分别为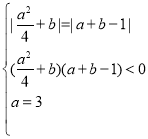 ,故
,故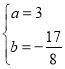 ,这与
,这与![]() 矛盾.
矛盾.
综上所述,当且仅当![]() ,
,![]() 时,对任意的
时,对任意的![]() ,恒有
,恒有![]() ,
,
故满足条件的所有实数对![]() 为
为![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙三位教师分别在一中、二中、三中三所中学里教不同的学科语文,数学,英语,已知:
①甲不在一中工作,乙不在二中工作;
②在一中工作的教师不教英语学科;
③在二中工作的教师教语文学科;
④乙不教数学学科.
可以判断乙工作地方和教的学科分别是________,_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】期末考试结束后,甲、乙、丙、丁四位同学预测数学成绩
甲:我不能及格.
乙:丁肯定能及格.
丙:我们四人都能及格.
丁:要是我能及格,大家都能及格.
成绩公布后,四人中恰有一人的预测是错误的,则预测错误的同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐代诗人杜牧的七绝唐诗《偶题》传诵至今,“道在人间或可传,小还轻变已多年。今来海上升高望,不到蓬莱不是仙” ,由此推断,后一句中“是仙”是“到蓬莱”的( )
A. 必要条件 B. 充分条件 C. 充要条件 D. 既非充分又非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于抽样的说法中正确的是( )
A. 已知总体容量为109,若要用随机数表法抽取一个容量为10的样本,可以将总体编号为000,001,002,003,…,108
B. 当总体、样本容量较大时,一般采用简单随机抽样
C. 当总体由有明显差异的几部分构成时,可以采用系统抽样
D. 在系统抽样的过程中,有时要剔除一些个体,所以在整个抽样过程中,每个个体被抽到的可能性不相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从4名男生和3名女生中推荐4人参加某高校自主招生考试,若这4人中必须既有男生又有女生,则不同的选法共有( )
A. 34 种 B. 35 种 C. 120 种 D. 140 种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加演讲社团 | 2 | 30 |
(I)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(II) 在既参加书法社团又参加演讲社团的8名同学中,有5名男同学![]() ,3名女同学
,3名女同学![]() ,现从这5名男同学和3名女同学中各随机选1人,求
,现从这5名男同学和3名女同学中各随机选1人,求![]() 被选中且
被选中且![]() 未被选中的概率。
未被选中的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com