
若S1=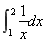 ,S2=
,S2=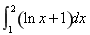 ,S3=
,S3= ,则S1,S2,S3的大小关系为( )
,则S1,S2,S3的大小关系为( )
A.S1<S2<S3 B.S2<S1<S3 C.S1<S3<S2 D.S3<S1<S2
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:044
设数列{an}的前n项和为sn,若s1=1,s2=2,且s n+1-3 s n+2 s n-1=0(n≥2且n∈N),试判断数列{an}是不是等比数列.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源:宁夏银川一中2012届高三第三次模拟考试数学理科试题 题型:044
已知点P是直角坐标平面内的动点,点P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且![]() .
.
(Ⅰ)求动点P所在曲线C的方程;
(Ⅱ)直线l过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线l1:x=-2的垂线,对应的垂足分别为M、N,试判断点F与以线段MN为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(Ⅲ)记S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),问是否存在实数λ,使S![]() =λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
=λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面几何里,有“若△ABC的三边长分别为a,b,c,内切圆半径为r,则三角形面积为S△ABC=![]() (a+b+c)r”,拓展到空间,类比上述结论,“若四面体ABCD的四个面的面积分别为S1,S2,S3,S4,内切球的半径为r,则四面体的体积为________”.
(a+b+c)r”,拓展到空间,类比上述结论,“若四面体ABCD的四个面的面积分别为S1,S2,S3,S4,内切球的半径为r,则四面体的体积为________”.
查看答案和解析>>
科目:高中数学 来源:2014届吉林省高二上学期期末考试理科数学试卷(解析版) 题型:填空题
若三角形的内切圆半径为r,三边的长分别为a,b,c,则三角形的面积S= r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com