解:(1)若a=0,则b=-c,f(0)•f(1)=c•(3a+2b+c)=-c
2≤0与已知矛盾∴a≠0…
由f(0)•f(1)>0,得c(3a+2b+c)>0
由条件a+b+c=0消去c,得(a+b)(2a+b)<0∵a
2>0∴
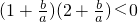
,∴
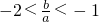
…
(2)方程3ax
2+2bx+c=0的判别式△=4(b
2-3ac)
由条件a+b+c=0消去b,得
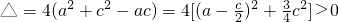
∴方程f(x)=0有实根
即函数f(x)的图象与x轴总有两个不同的交点A、B.设A(x
1,0),B(x
2,0)
由条件知
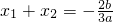
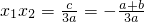
∴(x
1-x
2)
2=(x
1+x
2)
2-4x
1x
2=
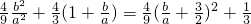
∵
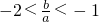
∴
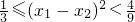
∴
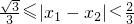
即
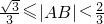
…
(3)设h(x)=f(x)-g(x)=ax
2+(b-a)x+c-b=ax
2-(2a+c)x+a+2c∵a>b>c,a+b+c=0∴a>0且a>-a-c>c
即
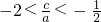
又h(x)的对称轴为
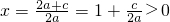
∴
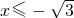
时,
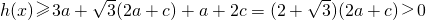
即
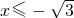
时,f(x)>g(x)恒成立…
分析:(1)先将f(0)>0,f(1)>0,利用函数式中的a,b,c进行表示,再结合等式关系利用不等式的基本性质即可得到a和

的范围即可.
(2)方程3ax
2+2bx+c=0的判别式△=4(b
2-3ac),由条件a+b+c=0消去b,证明其大于0,再利用韦达定理求线段AB|的取值范围
(3)先构建函数h(x)=f(x)-g(x)=ax
2+(b-a)x+c-b=ax
2-(2a+c)x+a+2c,再证明
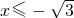
时,大于0即可.
点评:本题主要考查二次函数的基本性质与不等式的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

 <-1;
<-1;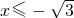 时,恒有f(x)>g(x).
时,恒有f(x)>g(x).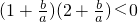 ,∴
,∴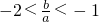 …
…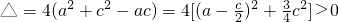 ∴方程f(x)=0有实根
∴方程f(x)=0有实根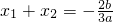
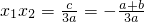 ∴(x1-x2)2=(x1+x2)2-4x1x2=
∴(x1-x2)2=(x1+x2)2-4x1x2=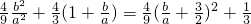 ∵
∵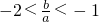 ∴
∴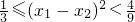 ∴
∴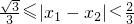 即
即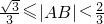 …
…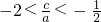
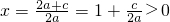
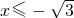 时,
时,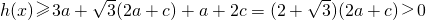
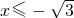 时,f(x)>g(x)恒成立…
时,f(x)>g(x)恒成立… 的范围即可.
的范围即可. 时,大于0即可.
时,大于0即可.
