练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若运行如图所示的程序框图，输出的的值为127，则输入的正整数的所有可能取值的个数为（ ）

    A. 8 B. 3 C. 2 D. 1

    【答案】B

    【解析】令,可得n=7,故输入n=7符合,当输入的n满足n>7时,输出的结果总是大于127,不合题意,当输入n=6,5,4时,输出的n值分别为,均不合题意,当输入n=3或n=2时,输出的n=127符合题意,当输入n=1时,将进入死循环不符,故输入的所有的n的可能取值为2,3,7,共3个,故选B.

    点睛: 本题考查程序框图的应用,属于中档题.算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某水域受到污染，水务部门决定往水中投放一种药剂来净化水质，已知每次投放质量为的药剂后，经过（）天，该药剂在水中释放的浓度（毫克升）为，其中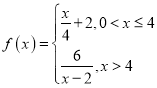，当药剂在水中释放浓度不低于（毫克升）时称为有效净化，当药剂在水中释放的浓度不低于（毫克升）且不高于（毫克升）时称为最佳净化.

    （1）如果投放的药剂质量为，那么该水域达到有效净化一共可持续几天？

    （2）如果投放的药剂质量为，为了使该水域天（从投放药剂算起，包括第天）之内都达到最佳净化，确定应该投放的药剂质量的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设:实数满足,其中;

    :实数满足.

    （Ⅰ）若,且为真,求实数的取值范围;

    （Ⅱ）若是的必要不充分条件,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（多选题）在数列中，若，（，，为常数），则称为“等方差数列”．下列对“等方差数列”的判断正确的是（ ）

    A.若是等差数列，则是等方差数列

    B.是等方差数列

    C.若是等方差数列，则（，为常数）也是等方差数列

    D.若既是等方差数列，又是等差数列，则该数列为常数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市春节期间7家超市的广告费支出（万元）和销售额（万元）数据如下：

    超市

    A

    B

    C

    D

    E

    F

    G

    广告费支出

    1

    2

    4

    6

    11

    13

    19

    销售额

    19

    32

    40

    44

    52

    53

    54

    （1）若用线性回归模型拟合与的关系，求关于的线性回归方程；

    （2）用二次函数回归模型拟合与的关系，可得回归方程：，经计算二次函数回归模型和线性回归模型的相关指数分别约为和，请用说明选择哪个回归模型更合适，并用此模型预测超市应支出多少万元广告费，能获得最大的销售额？最大的销售额是多少？（精确到个位数）

    参数数据及公式：，，．

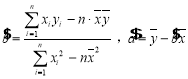    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲船在点发现乙船在北偏东的处，里，且乙船以每小时10里的速度向正北行驶，已知甲船的速度是每小时里，问：甲船以什么方向前进，才能与乙船最快相遇，相遇时甲船行驶了多少小时？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的上顶点为点，右焦点为.延长交椭圆于点，且满足.

    （1）试求椭圆的标准方程；

    （2）过点作与轴不重合的直线和椭圆交于两点，设椭圆的左顶点为点，且直线分别与直线交于两点，记直线的斜率分别为，则与之积是否为定值？若是，求出该定值；若不是，试说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）若有两个零点，求的范围；

    （2）若有两个极值点，求的范围；

    （3）在（2）的条件下，若的两个极值点为 ，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高二某班共有20名男生，在一次体验中这20名男生被平均分成两个小组，第一组和第二组男生的身高（单位： ）的茎叶图如下：

    （1）根据茎叶图，分别写出两组学生身高的中位数；

    （2）从该班身高超过的7名男生中随机选出2名男生参加校篮球队集训，求这2名男生至少有1人来自第二组的概率；

    （3）在两组身高位于（单位： ）的男生中各随机选出2人，设这4人中身高位于（单位： ）的人数为，求随机变量的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案