
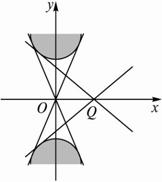
(1)画出9x2-16y2+144≤0对应的二次平面域;
(2)求x2+y2的最小值;
(3)求![]() 的取值范围.
的取值范围.
思路分析:本题可以使用线性规划的基本思路,像二元一次不等式所示的区域一样,我们仍然可以用“线定界,点定域”的方法来确定9x2-16y2+144≤0所表示的平面区域.
解:(1)将原点坐标代入9x2-16y2+144,其值为144>0,因此9x2-16y2+144≤0表示的平面区域如图所示的阴影部分,即双曲线![]() -
-![]() =1的含有焦点的区域.
=1的含有焦点的区域.
(2)设P(x,y)为该区域内任意一点,由上图可知,当P与双曲线的顶点(0,±4)重合时,|OP|取得最小值4.所以,x2+y2=|OP|2=16.
(3)取Q(2,0),则直线PQ的斜率为k=![]() ,其直线方程为y=k(x-2),代入9x2-16y2+144=0得(9-16k2)x2+64k2x-64k2+144=0,由Δ=0得k=±
,其直线方程为y=k(x-2),代入9x2-16y2+144=0得(9-16k2)x2+64k2x-64k2+144=0,由Δ=0得k=±![]() ,由图可知k≥
,由图可知k≥![]() 或k≤-
或k≤-![]() .
.
故所求![]() 的取值范围是(-∞,-
的取值范围是(-∞,- ![]() ]∪[
]∪[![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
| 7π |
| 6 |
| 11π |
| 6 |
| 7π |
| 6 |
| 11π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(必修5) 2009-2010学年 第11期 总第167期 北师大课标版(必修5) 题型:013
若
x,y满足一元二次不等式组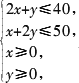 则z=3x+2y的最大值是
则z=3x+2y的最大值是
90
80
70
40
查看答案和解析>>
科目:高中数学 来源: 题型:044
(1)画出9x2-16y2+144≤0对应的二次平面域;
(2)求x2+y2的最小值;
(3)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:设计必修五数学人教A版 人教A版 题型:044
若把满足二元二次不等式(组)的平面区域叫做二次平面域.
(1)画出9x2-16y2+144≤0对应的二次平面域;
(2)求x2+y2的最小值;
(3)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com